
【题目】如图所示是一种棱长分别为3cm,4cm,5cm的长方体积木,现要用若干块这样的积木来搭建大长方体,如果用3块来搭,那么搭成的大长方体表面积最小是_____cm,如果用4块来搭,那么搭成的大长方体表面积最小是_____cm,如果用12块来搭,那么搭成的大长方体表面积最小是_____cm.
![]()
【答案】202 258 484.
【解析】
如果用3块来搭,那么搭成的大长方体表面积最小是长3×3=9cm,宽4cm,高5cm的长方体的表面积,根据长方体的表面积公式即可求解;如果用4块来搭,那么搭成的大长方体表面积最小是长4×2=8cm,宽3×2=6cm,高5cm的长方体的表面积,根据长方体的表面积公式即可求解;如果用12块来搭,那么搭成的大长方体表面积最小是长3×3=9cm,宽4×2=8cm,高5×2=10cm的长方体的表面积,根据长方体的表面积公式即可求解.
长3×3=9cm,宽4cm,高5cm,
(9×4+9×5+4×5)×2
=(36+45+20)×2
=101×2
=202(cm2).
答:如果用3块来搭,那么搭成的大长方体表面积最小是202cm2.
长4×2=8cm,宽3×2=6cm,高5cm,
(9×6+9×5+6×5)×2
=(54+45+30)×2
=129×2
=258(cm2).
答:如果用4块来搭,那么搭成的大长方体表面积最小是258cm2.
长3×3=9cm,宽4×2=8cm,高5×2=10cm,
(9×8+9×10+8×10)×2
=(72+90+80)×2
=242×2
=484(cm2).
答:如果用12块来搭,那么搭成的大长方体表面积最小是484cm2.
故答案为:202;258;484.


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0), B(0,﹣1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
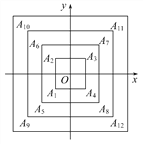
【题目】如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…,则顶点A20的坐标为 ( )
A. (5,5) B. (5,-5) C. (-5,5) D. (-5,-5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011贵州安顺,9,3分)正方形ABCD边长为1,E、F、G、H分别为边AB、BC、CD、DA上的点,且AE=BF=CG=DH.设小正方形EFGH的面积为y,AE=x. 则y关于x的函数图象大致是( )

A. B. C. D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB与CD相交于点O,OE是∠BOD的平分线

(1)∠DOE的补角有 ;
(2)若∠DOE:∠AOD=1:7,求∠AOC的度数;
(3)射线OF⊥OE.
①当射线OF在直线AB上方时,试探究∠BOC与∠DOF之间的数量关系,并说明理由;
②当射线OF在直线AB下方时,∠BOC与∠DOF之间的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学问题:计算等差数列5,2,﹣1,﹣4……前n项的和.
问题探究:为解决上面的问题,我们从最简单的问题进行探究.
探究一:首先我们来认识什么是等差数列.
数学上,称按一定顺序排列的一列数为数列,其中排在第一位的数称为第1项,用a1表示:排在第二位的数称为第2项,用a2表示……排在第n位的数称为第n项,用an表示.一般地,如果一个数列从第二项起,每一项与它的前一项的差都等于同一个常数,那么这个数列叫做等差数列,这个常数叫等差数列的公差,公差通常用字母d表示.如:数列2,4,6,8,….为等差数列,其中a1=2,公差d=2.
(1)已知等差数列5,2,﹣1,﹣4,…则这个数列的公差d= ,第5项是 .
(2)如果一个数列a1,a2,a3,a4,…是等差数列,且公差为d,那么根据定义可得到:
a2﹣a1=d,a3﹣a2=d,a4﹣a3=d,……an﹣an﹣1=d,所以a2=a1+d,a3=a2+d=a1+2d,a4=a1+3d,……:由此可得an= (用a1和d的代数式表示)
(3)对于等差数列5,2,﹣1,﹣4,…,an= 请判断﹣2020是否是此等差数列的某一项,若是,请求出是第几项:若不是,说明理由.
探究二:二百多年前,数学王子高斯用他独特的方法快速计算出1+2+3+4+…+100的值.我们从这个算法中受到启发,用此方法计算数列1,2,3,…,n的前n项和:由 可知
可知![]()
(4)请你仿照上面的探究方式,解决下面的问题:
若a1,a2,a3,…,an为等差数列的前n项,前n项和Sn=a1+a2+a3+…+an.证明:Sn=na1+![]() .
.
(5)计算:计算等差数列5,2,﹣1,﹣4…前n项的和Sn(写出计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)
(1)如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进货价为每件30元,为了合理定价,先投放市场试销.据市场调查,销售价为每件40元时,每周的销售量是180件,而销售价每上涨1元,则每周的销售量就会减少5件,设每件商品的销售价上涨x元,每周的销售利润为y元.
(1)用含x的代数式表示:每件商品的销售价为 元,每件商品的利润为 元,每周的商品销售量为 件;
(2)求y关于x的函数关系式(不要求写出x的取值范围);
(3)应怎样确定销售价,使该商品的每周销售利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com