B
分析:根据等式的性质对每个选项注意论证,得出正确选项.
解答:A、ac=bc,当c=0时,a≠b时,ac=bc也成立,故若ac=bc,则a=b不正确;
B、若
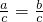
,c不能为0,由等式的性质得:a=b,故若
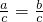
,则a=b正确;
C、若|a|=|b|,则a=b,如果a和b互为相反数时,也有|a|=|b|,即a=-b,故若|a|=|b|,则a=b不正确;
D、如果a和b互为相反数即a=-b时,也有a
2=b
2,故若a
2=b
2,则a=b不正确.
故选B.
点评:此题考查的知识点是等式的性质,本题关键是注意互为相反数的两个数的绝对值及平方数相等.

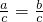 ,则a=b
,则a=b