
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 4x2y+xy+3xy2=xy(4x+3y) | B. | $\frac{1}{4}$a2+ab+b2=$\frac{1}{4}$(a+2b)2 | ||
| C. | m2+4=(m+2)2 | D. | 若x2-x+42=(x+a)(x+b),则a,b异号 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3)2的算术平方根是3 | B. | $\sqrt{225}$的平方根是±15 | ||
| C. | 当x=0或2时,x$\sqrt{x-2}$=0 | D. | $\frac{\sqrt{3}}{2}$是分数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
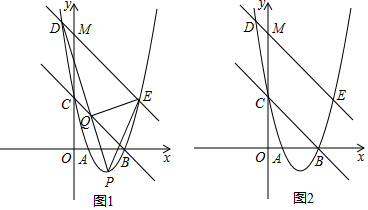
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
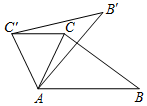 如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A按逆时针方向旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'=( )
如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A按逆时针方向旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'=( )| A. | 30° | B. | 35° | C. | 40° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
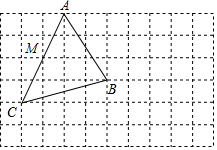 如图,在边长为1的正方形网格中有△ABC,请按下列要求画图并解答问题.
如图,在边长为1的正方形网格中有△ABC,请按下列要求画图并解答问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com