
【题目】如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD的长为____.

【答案】2
【解析】过P作PE垂直与OB,由∠AOP=∠BOP,PD垂直于OA,利用角平分线定理得到PE=PD,由PC与OA平行,根据两直线平行得到一对内错角相等,又OP为角平分线得到一对角相等,等量代换可得∠COP=∠CPO,又∠ECP为三角形COP的外角,利用三角形外角的性质求出∠ECP=30°,在直角三角形ECP中,由30°角所对的直角边等于斜边的一半,由斜边PC的长求出PE的长,即为PD的长.
解:过P作PE⊥OB,交OB与点E,
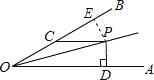

∵∠AOP=∠BOP,PD⊥OA,PE⊥OB,
∴PD=PE,
∵PC∥OA,
∴∠CPO=∠POD,
又∠AOP=∠BOP=15°,
∴∠CPO=∠BOP=15°,
又∠ECP为△OCP的外角,
∴∠ECP=∠COP+∠CPO=30°,
在直角三角形CEP中,∠ECP=30°,PC=4,
∴PE=![]() PC=2,
PC=2,
则PD=PE=2.
故答案为:2.


科目:初中数学 来源: 题型:
【题目】下列四个命题中,真命题有( )
①两条直线被第三条直线所截,内错角相等;
②如果∠1和∠2是对顶角,那么∠1=∠2;
③三角形的一个外角大于任何一个内角;
④若a2=b2,则a=b.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( ) 
A.35°
B.45°
C.55°
D.65°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在正方形网格中,每个小方格都是边长为1的正方形,A和B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且以A,B,C为顶点的三角形的面积为1个平方单位,则C点的个数为( ). 
A.3个
B.4个
C.5个
D.6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N,
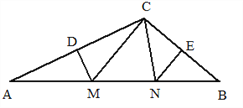
(1)若△CMN的周长为21cm,求AB的长;
(2)若∠MCN=50°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.
(1)求证:△AEB≌△CFD;
(2)若四边形EBFD是菱形,求∠ABD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】挑战自我!
下图是由一些火柴棒搭成的图案: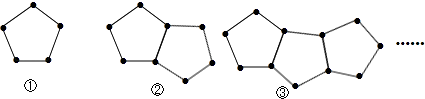
(1)摆第①个图案用几根火柴棒,
摆第②个图案用几根火柴棒,
摆第③个图案用几根火柴棒.
(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒?
(3)计算一下摆121根火柴棒时,是第几个图案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发沿图中某一个扇形顺时针匀速运动,设∠APB=y(单位:度),如果y与点P运动的时间x(单位:秒)的函数关系的图象大致如图2所示,那么点P的运动路线可能为( )

A.O→B→A→O B.O→A→C→O C.O→C→D→O D.O→B→D→O
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com