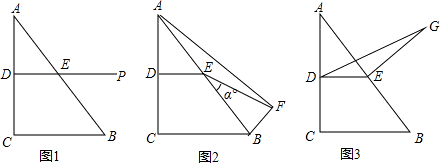
解:(1)∵四边形BCDF是矩形,
∴DP=BC=6,
∵点D、E分别是边AC、AB的中点,
∴DE=

BC=3,
∴EP=6-3=3,
故答案为:3;
(2)①∵点E是边AB的中点,
∴AE=BE,
∵根据旋转的性质可得,BE=EF,
∴BE=EF=AE,
在△BEF中,∠BEF=α°,可得∠EBF=∠BFE=

(180°-α°)=90°-

α°,
在△AEF中,可得∠EAF=∠AFE=

∠FEB=

α°,
∴∠BFE+∠AFE=90°-

α°+

α°=90°,
∴△ABF是直角三角形;
②过点E作EK⊥BC,垂足为点K,过点G作GM⊥DE交DE延长线于M,

∵点D、E分别是边AC、AB的中点,
∴DE∥BC,
∵∠C=90°,
∴∠EDC=90°,
∵∠C=90°,EK⊥BC,GM⊥DE,
∴∠M=∠EKB═90°,EK∥DC,
∴∠MEK=∠EDC=90°,
∴∠MEB+∠BEK=90°,
∵EG⊥AB,
∴∠GEB=90°,
∴∠GEM+∠MEB=90°,
∴∠GEM=∠BEK,
∵将点B绕点E逆时针旋转到G,
∴EG=BE,
在△GME和△BKE中
∵
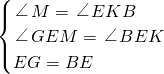
,
∴△GME≌△BKE(AAS),
∴GM=BK,
∵∠C=∠EKC=∠EDC=90°,
∴四边形DCKE是矩形,
∴DE=CK=3,
∴GM=BK=6-3=3,
∴△DEG的面积为

DE×GM=

×3×3=

.
分析:(1)根据矩形性质得出DP=BC,根据三角形中位线求出DE=3,即可得出答案;
(2)①根据旋转得出AE=EF=BE,得出∠FAE=∠EFA=

α°,∠EFB=∠EBF=90°-

α°,求出∠AFB的度数,即可得出答案;
②过点E作EK⊥BC,垂足为点K,过点G作GM⊥DE交DE延长线于M,求出BE=EG,∠GME=∠EKB=90°,∠GEM=∠BEK,根据AAS证△GME≌△BKE,推出GM=BK,求出BK,根据三角形的面积公式求出即可.
点评:本题综合考查了全等三角形的性质和判定,旋转的性质,等腰三角形的性质和判定,三角形的内角和定理,三角形的中位线定理等知识点,主要考查学生综合运用性质进行推理的能力,本题综合性比较强,有一定的难度.

 BC=3,
BC=3, (180°-α°)=90°-
(180°-α°)=90°- α°,
α°, ∠FEB=
∠FEB= α°,
α°, α°+
α°+ α°=90°,
α°=90°,
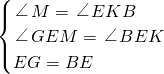 ,
, DE×GM=
DE×GM= ×3×3=
×3×3= .
. α°,∠EFB=∠EBF=90°-
α°,∠EFB=∠EBF=90°- α°,求出∠AFB的度数,即可得出答案;
α°,求出∠AFB的度数,即可得出答案;

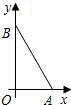 已知一个直角三角形纸片OAB,其中∠AOB=90°,OA=2,OB=4.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB交于点C,与边AB交于点D.
已知一个直角三角形纸片OAB,其中∠AOB=90°,OA=2,OB=4.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB交于点C,与边AB交于点D.