
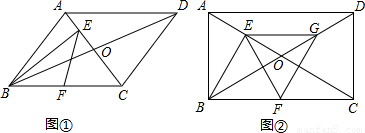
 BC,求出EG∥BC,EG=
BC,求出EG∥BC,EG= BC,求出BF=EG,BF∥EG,EG=GF,得出平行四边形,根据菱形的判定推出即可.
BC,求出BF=EG,BF∥EG,EG=GF,得出平行四边形,根据菱形的判定推出即可.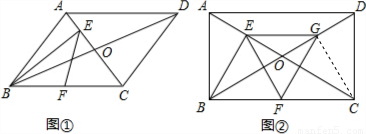
 BC=
BC= AD,
AD, AD,
AD, BC,
BC, BC,EG=GF,
BC,EG=GF,

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
 =∠DCE.
=∠DCE.| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 在下面推理过程的括号内填上推理的依据
在下面推理过程的括号内填上推理的依据| ∥ | . |
查看答案和解析>>
科目:初中数学 来源:同步训练与评价·数学·八年级·上 题型:022
(1)一个四边形只要具有下列条件之一,就是平行四边形:①两组对边________;②两组对角________;③两条对角线________;④一组对边________.
(2)在四边形ABCD中,当∠A+∠B=![]() 、∠B+∠C=
、∠B+∠C=![]() 时,边AB与CD的关系是________.
时,边AB与CD的关系是________.
(3)在![]() ABCD中,∠BAC=
ABCD中,∠BAC=![]() ,∠BCA=
,∠BCA=![]() ,则∠B=________.
,则∠B=________.
查看答案和解析>>
科目:初中数学 来源: 题型:022
(2004·广西桂林)如图如示,在ABCD中,BD是对角线,E、F是对角在线的两点,要使△BCF≌△DAE,还需添加一个条件(只需添加一个条件)是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com