
 如图是一个横放的油桶的横截面图,油的最大深度为30cm,油面宽度为60$\sqrt{3}$cm,则油面的面积为( )cm2.
如图是一个横放的油桶的横截面图,油的最大深度为30cm,油面宽度为60$\sqrt{3}$cm,则油面的面积为( )cm2.| A. | 2400π-1800$\sqrt{3}$ | B. | 2400π-900$\sqrt{3}$ | C. | 1200π-900$\sqrt{3}$ | D. | π-1800$\sqrt{3}$ |
分析 先过点O作OD⊥AB于点D,连接OA,由垂径定理可知AD=$\frac{1}{2}$AB,设OA=r,则OD=r-30,在Rt△AOD中,利用勾股定理即可求出r的值于是得到结论.
解答 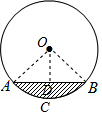 解:过点O做OC⊥AB于点D,连接OA,OB.
解:过点O做OC⊥AB于点D,连接OA,OB.
设半径长为rcm,
∵OC⊥AB,
∴AD=$\frac{1}{2}$AB
=$\frac{1}{2}$×60$\sqrt{3}$
=30$\sqrt{3}$(cm),
∵CD=30cm,∴OD=r-30(cm)
在Rt△AOD中,由勾股定理得:(r-30)2+(30$\sqrt{3}$)2=r2
∴r=60,
∴∠AOD=60°,
∴∠AOB=120°,
∴油面的面积为=S扇形-S△AOB=1200π-900$\sqrt{3}$,
故选C.
点评 本题考查的是垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:选择题
 如图,张亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
如图,张亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )| A. | 经过一点有无数条直线 | B. | 经过两点,有且仅有一条直线 | ||
| C. | 两点间距离的定义 | D. | 两点之间,线段最短 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
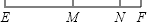 如图,M是线段EF的中点,N是线段MF上一点,如果EF=2a,NF=b,那么下面结论中错误的是( )
如图,M是线段EF的中点,N是线段MF上一点,如果EF=2a,NF=b,那么下面结论中错误的是( )| A. | MN=a-b | B. | MN=$\frac{1}{2}$a | C. | EM=a | D. | EN=2a-b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查华为手机的使用寿命 | |
| B. | 调查你班学生打网络游戏的情况 | |
| C. | 调查平顶山市七年级学生的心理健康情况 | |
| D. | 中央电视台财经频道《是真的吗》的节目收视率 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com