
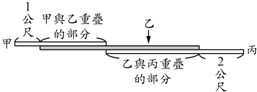
 如图为甲、乙、丙三根笔直的木棍平行摆放在地面上的情形.已知乙有一部分只与甲重迭,其余部分只与丙重迭,甲没有与乙重迭的部分的长度为1公尺,丙没有与乙重迭的部分的长度为2公尺.若乙的长度最长且甲、乙的长度相差x公尺,乙、丙的长度相差y公尺,则乙的长度为多少公尺?( )
如图为甲、乙、丙三根笔直的木棍平行摆放在地面上的情形.已知乙有一部分只与甲重迭,其余部分只与丙重迭,甲没有与乙重迭的部分的长度为1公尺,丙没有与乙重迭的部分的长度为2公尺.若乙的长度最长且甲、乙的长度相差x公尺,乙、丙的长度相差y公尺,则乙的长度为多少公尺?( )| A. | x+y+3 | B. | x+y+1 | C. | x+y-1 | D. | x+y-3 |
分析 设乙的长度为a公尺,则甲的长度为:(a-x)公尺;丙的长度为:(a-y)公尺,甲与乙重叠的部分长度为:(a-x-1)公尺;乙与丙重叠的部分长度为:(a-y-2)公尺,由图可知:甲与乙重叠的部分长度+乙与丙重叠的部分长度=乙的长度,列出方程(a-x-1)+(a-y-2)=a,即可解答.
解答 解:设乙的长度为a公尺,
∵乙的长度最长且甲、乙的长度相差x公尺,乙、丙的长度相差y公尺,
∴甲的长度为:(a-x)公尺;丙的长度为:(a-y)公尺,
∴甲与乙重叠的部分长度为:(a-x-1)公尺;乙与丙重叠的部分长度为:(a-y-2)公尺,
由图可知:甲与乙重叠的部分长度+乙与丙重叠的部分长度=乙的长度,
∴(a-x-1)+(a-y-2)=a,
a-x-1+a-y-2=a,
a+a-a=x+y+1+2,
a=x+y+3,
∴乙的长度为:(x+y+3)公尺,
故选:A.
点评 本题考查了考查了二元一次方程的应用,解决本题的关键是根据图形找到等量关系,列方程.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的边长为2,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为2-$\sqrt{2}$.
如图,正方形ABCD的边长为2,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为2-$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
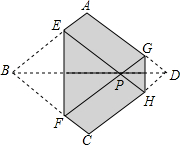 如图,菱形纸片ABCD的边长为2,折叠菱形纸片,将B、D两点重合在对角线BD上的同一点P处,折痕分别为EF、GH.重合点P在对角线BD上移动,设折痕EF的长为m.请你分别判断以下结论的真假,并给出理由.
如图,菱形纸片ABCD的边长为2,折叠菱形纸片,将B、D两点重合在对角线BD上的同一点P处,折痕分别为EF、GH.重合点P在对角线BD上移动,设折痕EF的长为m.请你分别判断以下结论的真假,并给出理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com