Question

如图，在锐角三角形ABC中，，△ABC的面积为48，D，E分别是边AB，AC上的两个动点（D不与，重合），且保持DE∥BC，以DE为边，在点的异侧作正方形DEFG.

（1）当正方形DEFG的边GF在BC上时，求正方形DEFG的边长；

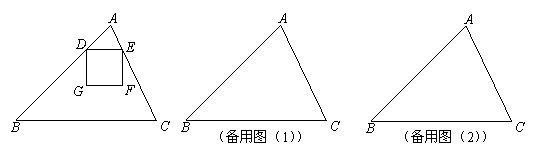（2）设DE = x，△ABC与正方形DEFG重叠部分的面积为，试求关于的函数关系式，写出x的取值范围，并求出y的最大值.

Answer 1

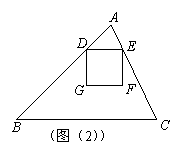
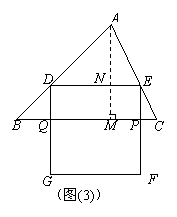
解：（1）当正方形DEFG的边GF在BC上时，如图

（1），过点A作BC边上的高AM，交DE于N，垂足为M.

∵S_△ABC=48，BC=12，∴AM=8.

∵DE∥BC，△ADE∽△ABC,

∴，

而AN=AM－MN=AM－DE，∴. 

解之得.

∴当正方形DEFG的边GF在BC上时，正方形DEFG的边长为4.8.…3分

 

（2）分两种情况：

①当正方形DEFG在△ABC的内部时，如图（2），△ABC与正方形DEFG重叠部分的面积为正方形DEFG的面积，∵DE=x，∴，此时x的范围是≤4.8

 

②当正方形DEFG的一部分在△ABC的外部时，

如图（2），设DG与BC交于点Q，EF与BC交于点P，

△ABC的高AM交DE于N，

∵DE=x，DE∥BC，∴△ADE∽△ABC,

即，而AN=AM－MN=AM－EP,

∴，解得.

所以,  即.

由题意，x>4.8，x<12,所以.

因此△ABC与正方形DEFG重叠部分的面积为

(0< x≤4.8)

   

当≤4.8时，△ABC与正方形DEFG重叠部分的面积的最大值为4.8²=23.04

当时，因为，所以当时，

△ABC与正方形DEFG重叠部分的面积的最大值为.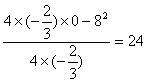

因为24>23.04，

所以△ABC与正方形DEFG重叠部分的面积的最大值为24.