已知二次函数的图象过A(-3,0)、B(1,0)两点.
(1)当这个二次函数的图象又过点C(0,3)时,求其解析式.
(2)设(1)中所求二次函数图象的顶点为P,求S△APC:S△ABC的值.
(3)如果二次函数图象的顶点M在对称轴上移动,并与y轴交于点D,S△AMD:S△ABD的值确定吗?为什么?
分析:(1)已知了抛物线上A、B、C三点的坐标,可用待定系数法求出抛物线的解析式.
(2)先根据抛物线的解析式求出P点的坐标,由于△APC的面积无法直接求出,因此可用四边形AOCP的面积(梯形PCNO的面积+△APN的面积)-△AOC的面积来求得.△ABC中,已知了A、B、C三点的坐标,即可根据三角形面积公式求出其面积.据此可求出两三角形的面积比.
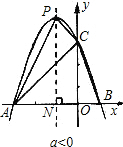
(3)可用交点式二次函数通式来设出抛物线的解析式,然后表示出其顶点M的坐标,按(2)的方法分别求出△AMD和△ABD的面积.进行比较即可(要注意二次函数二次项系数的符号要分正负两种情况进行讨论).
解答: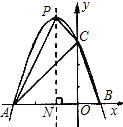
解:(1)设二次函数的解析式为:y=a(x-x
1)(x-x
2)
∵二次函数的图象过A(-3,0)、B(1,0)两点
∴y=a(x+3)(x-1)
∵二次函数的图象过点C(0,3)
∴3=a(0+3)(0-1)
∴a=-1
∴所求二次函数的解析式为:y=-x
2-2x+3
(2)∵y=-x
2-2x+3
∴P的坐标为(-1,4)
过点P作二次函数图象的对称轴交x轴于N
∵S
△APC=S
梯形PNOC+S
△APN-S
△AOC=
(OC+PN)•ON+
AN•PN-
OA•OC=
(3+4)×1+
×2×4-
×3×3=3
S△ABC=
AB•OC=
×4×3=6
∴S
△APC:S
△ABC=3:6=1:2;
(3)设此二次函数的解析式为:y=a(x+3)(x-1)=ax
2+2ax-3a
∴D(0,-3a)
∵点M在对称轴x=-1上,且在函数图象上
∴M(-1,-4a)
当a=0时,即顶点在对称轴与x轴的交点处,函数图象不存在
∴S
△AMD:S
△ABD的值不存在.
当a≠0时,S
△AMD=S
梯形ODMN+S
△AMN-S
△AOD=
(OD+MN)•ON+
AN•MN-
OA•OD
=
(|-3a|+|-4a|)×1+
×2×|-4a|-
×3×|-3a|
=
|-4a|-|-3a|
S
△ABD=
AB•OD=
×4×|-3a|=2|-3a|
∴
=当a<0时:
===当a>0时:
===∴当a≠0时,S
△AMD:S
△ABD的值是确定的.
点评:本题考查了二次函数解析式的确定、图形的面积求法等知识及综合应用知识、解决问题的能力.要注意(3)中a的符号不确定时,要分类进行讨论.

 解:(1)设二次函数的解析式为:y=a(x-x1)(x-x2)
解:(1)设二次函数的解析式为:y=a(x-x1)(x-x2)


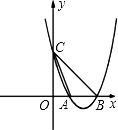 已知二次函数的图象过点(4,3),它的顶点坐标是(2,-1).
已知二次函数的图象过点(4,3),它的顶点坐标是(2,-1).