
如图,点P是直线![]() :
:![]() 上的点,过
上的点,过![]() 点P的另一条直线
点P的另一条直线![]() 交抛物线
交抛物线![]() 于A、B两点.
于A、B两点.
(1)若直线![]() 的解析式为
的解析式为![]() ,求A、B两点的坐标;
,求A、B两点的坐标;
(2)①若点P的坐标为(-2,![]() ),当PA=AB
),当PA=AB![]() 时,请直接写出点A的坐标;
时,请直接写出点A的坐标;
②试证明:对于直线![]() 上任意给定的一点P,在抛物线上都能找到点A,使得PA=AB成立.
上任意给定的一点P,在抛物线上都能找到点A,使得PA=AB成立.


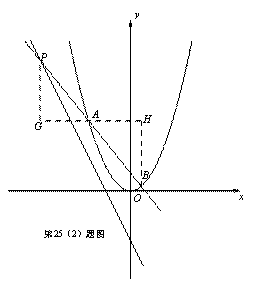
 (3)设直线
(3)设直线![]() 交
交![]() 轴于点C,若△AOB的外心在边AB上,且∠BPC=∠OCP,求点P的坐标.
轴于点C,若△AOB的外心在边AB上,且∠BPC=∠OCP,求点P的坐标.
解:(1)依题意,得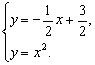 解得
解得 ,
,![]()
∴A(![]() ,
,![]() ),B(1,1).
),B(1,1).
(2)①A1(-1,1),A2(-3,9).
②过点P、B分别作过点A且平行于![]() 轴的直线的垂线,垂足分别为G、H.
轴的直线的垂线,垂足分别为G、H.
设P(![]() ,
,![]() ),A(
),A(![]() ,
,![]() ),∵PA=PB,∴△PAG≌△BAH,
),∵PA=PB,∴△PAG≌△BAH,
∴AG=AH,PG=BH,∴B(![]() ,
,![]() ),
),
将点B坐标代入抛物线![]() ,得
,得![]() ,
,
∵△=![]()
∴无论![]() 为何值时,关于
为何值时,关于![]() 的方程总有两个不等的实数解,即对于任意给定的
的方程总有两个不等的实数解,即对于任意给定的
点P,抛物线上总能找到两个满足条件的点A.
(3)设直线![]() :
:![]() 交y轴于D,设A(
交y轴于D,设A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ).
).
过A、B两点分别作AG、BH垂直![]() 轴于G、H.
轴于G、H.
∵△AOB的外心在AB上,∴∠AOB=90°,
由△AGO∽△OHB,得![]() ,∴
,∴![]() .
.
联立![]() 得
得![]() ,依题意,得
,依题意,得![]() 、
、![]() 是方程
是方程![]() 的两根,∴
的两根,∴![]() ,∴
,∴![]() ,即D(0,1).
,即D(0,1).
∵∠BPC=∠OCP,∴DP=DC=3.P
设P(![]() ,
,![]() ),过点P作PQ⊥
),过点P作PQ⊥![]() 轴于Q,在Rt△PDQ中,
轴于Q,在Rt△PDQ中,![]() ,
,
∴![]() .∴
.∴![]() (舍去),
(舍去),![]() ,∴P(
,∴P(![]() ,
,![]() ).
).
 ∵PN平分∠MNQ,∴PT=NT,∴
∵PN平分∠MNQ,∴PT=NT,∴![]() ,
,
 |


科目:初中数学 来源: 题型:
 20、如图,点O是直线AB上一点,OC平分∠AOB,在直线AB另一侧以O为顶点作∠DOE=90°
20、如图,点O是直线AB上一点,OC平分∠AOB,在直线AB另一侧以O为顶点作∠DOE=90°查看答案和解析>>
科目:初中数学 来源: 题型:
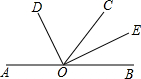 如图,点O是直线AB上一点,OC是任一条射线,OD、OE分别是∠AOC和∠BOC的平分线,则∠BOD的补角是
如图,点O是直线AB上一点,OC是任一条射线,OD、OE分别是∠AOC和∠BOC的平分线,则∠BOD的补角是查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点0是直线AB上一点.∠AOE=∠FOD=90°,OD平分∠EOC,
如图,点0是直线AB上一点.∠AOE=∠FOD=90°,OD平分∠EOC,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com