
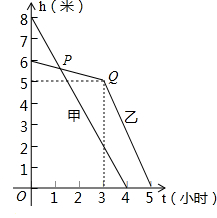
 甲、乙两个水池同时放水,其水面高度(水面离池底的距离)h(米)与时间t(小时)之间的关系如图所示(甲、乙两个水池底面相同).
甲、乙两个水池同时放水,其水面高度(水面离池底的距离)h(米)与时间t(小时)之间的关系如图所示(甲、乙两个水池底面相同).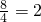 (米/小时).
(米/小时). (米/小时);
(米/小时); (米/小时).
(米/小时). <2,2<
<2,2< ,
,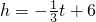 .
.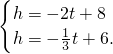 解得
解得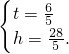 所以
所以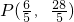 ,即P(1.2,5.6).
,即P(1.2,5.6).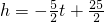 .
. ,即h=2.5.
,即h=2.5.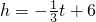 .两者相等即可求出p点坐标;
.两者相等即可求出p点坐标; ,
,

科目:初中数学 来源: 题型:
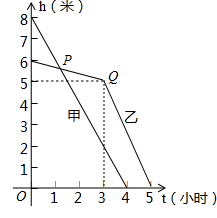 甲、乙两个水池同时放水,其水面高度(水面离池底的距离)h(米)与时间t(小时)之间的关系如图所示(甲、乙两个水池底面相同).
甲、乙两个水池同时放水,其水面高度(水面离池底的距离)h(米)与时间t(小时)之间的关系如图所示(甲、乙两个水池底面相同).查看答案和解析>>
科目:初中数学 来源: 题型:
 (m3)与放水时间x(h)的关系如图所示.已知乙水池容量比甲水池容量少5m3.请根据下图所提供的信息解答下列问题:
(m3)与放水时间x(h)的关系如图所示.已知乙水池容量比甲水池容量少5m3.请根据下图所提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
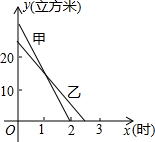 、乙两蓄水池中剩余水量y(立方米)与放水时间x(小时)之间的关系如图所示,已知y乙=-10x+25.
、乙两蓄水池中剩余水量y(立方米)与放水时间x(小时)之间的关系如图所示,已知y乙=-10x+25.查看答案和解析>>
科目:初中数学 来源:2011年湖北省襄阳市老河口市中考数学模拟试卷(3月份)(解析版) 题型:解答题
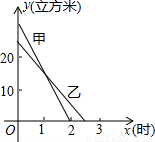
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com