

 ∠ADO=22.5°,
∠ADO=22.5°,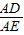 ,因为AE=EF<BE,
,因为AE=EF<BE, AB,所以tan∠AED=
AB,所以tan∠AED= >2,因此②错.
>2,因此②错.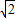 ,BD=2+
,BD=2+ ,DF=1+
,DF=1+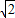 ,
,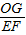 =
=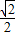 ,
,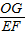 =
= =
=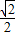 ,
,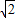 EF=2OG,
EF=2OG,

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源:2008年全国中考数学试题汇编《代数式》(04)(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2009年江西省宜春市高安二中中考数学二模试卷(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2009年湖北省孝感市市直五校三月联考数学试卷(文昌中学 张大勇、田禅心)(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2009年海南省初中毕业生模拟考试数学科试卷(海口十中 吴坤雄)(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com