Question

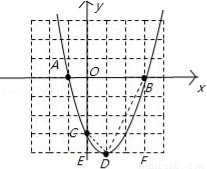
已知二次函数y＝x2－2x－3的图象与x轴交于A、B两点（A在B的左侧）,与y轴交于点C,顶点为D．

（1）求点A、B、C、D的坐标,并在下面直角坐标系中画出该二次函数的大致图象;

（2）说出抛物线y＝x2－2x－3可由抛物线y＝x2如何平移得到？

（3）求四边形OCDB的面积．

 

Answer 1

【答案】

（1）A（﹣1,0）,B（3,0）,C（0,﹣3）,D（1,﹣4）图形见解析;

（2）抛物线y＝x2－2x－3可由y＝x2先向右平移1个单位,再向下平移4个单位而得到;

（3）四边形OCDB的面积为．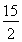

【解析】

试题分析:（1）先把此二次函数化为y=（x+1）（x﹣3）的形式,即可求出A、B两点的坐标,由二次函数的解析式可知c=﹣3,故可知C点坐标,由二次函数的顶点式即可求出其顶点坐标;

（2）根据四边形OCDB的面积=S矩形OEFB﹣S△BDF﹣S△CED即可解答．

试题解析:（1）∵二次函数y=x2﹣2x﹣3可化为y=（x+1）（x﹣3）,A在B的左侧,

∴A（﹣1,0）,B（3,0）,

∵c=﹣3,

∴C（0,﹣3）,

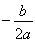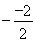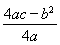∵x===1,y==﹣4,

∴D（1,﹣4）,故此函数的大致图象为:

（2）抛物线y＝x2－2x－3可由y＝x2先向右平移1个单位,再向下平移4个单位而得到;

（3）连接CD、BD,

则四边形OCDB的面积=S矩形OEFB﹣S△BDF﹣S△CED

=OB•|OE|﹣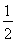DF•|BF|﹣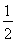DE•CE

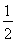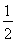=3×4﹣×2×4﹣×1×1

=12﹣4﹣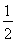

=．

．

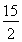考点:二次函数图象上点的坐标特征．