

分析 (1)首先求出A、B两点坐标,根据tan∠DAO=$\frac{3}{4}$=$\frac{DO}{AO}$,求出OD,设直线AD解析式为y=kx+b,列出方程组即可解决问题.
(2)如图1中,在点P移动过程中,∠PEG的大小不变,所以PE最长时,△PEG的周长最大,求出此时点P坐标,再根据S四边形GEFH=S△PGE-S△PFH,即可解决问题.
(3)如图2中,作QH⊥AD于H,旋转后H的对应点为H′.设M点坐标(m,$\frac{3}{4}$m+$\frac{3}{2}$).由△QHD≌△QH′N,推出DQ=QN,推出四边形QDMN是菱形,利用方程组求出点Q坐标,列出方程即可解决问题.
解答 解:(1)令y=0,则$\frac{3}{8}$x2-$\frac{3}{4}$x-3=0,解得x=-2或4,
∴A(-2,0),B(4,0),
∴OA=2,
∵tan∠DAO=$\frac{3}{4}$=$\frac{DO}{AO}$,
∴OD=$\frac{3}{2}$,
∴点D坐标(0,$\frac{3}{2}$),
设直线AD解析式为y=kx+b,则有$\left\{\begin{array}{l}{b=\frac{3}{2}}\\{-2k+b=0}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=\frac{3}{2}}\end{array}\right.$,
∴直线AD解析式为y=$\frac{3}{4}$x+$\frac{3}{2}$.
(2)如图1中,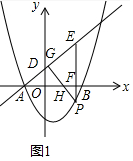
∵在点P移动过程中,∠PEG的大小不变,
∴PE最长时,△PEG的周长最大,
设P(m,$\frac{3}{8}$m2-$\frac{3}{4}$m-3),则E(m,$\frac{3}{4}$m+$\frac{3}{2}$),
∴PE=$\frac{3}{4}$m+$\frac{3}{2}$-($\frac{3}{8}$m2-$\frac{3}{4}$m-3)=-$\frac{3}{8}$m2+$\frac{3}{2}$m+$\frac{9}{2}$=-$\frac{3}{8}$(m-2)2+6,
∵-$\frac{3}{8}$<0,
∴m=2时,PE最长,△PEG的周长最长,
此时P(2,-3),E(2,3),F(2,0),
∵OD∥PE,
∴∠ADO=∠PEG,∵∠AOD=∠PGE,
∴△AOD∽△PGE,
∴$\frac{AO}{PG}$=$\frac{DO}{EG}$=$\frac{AD}{PE}$,
∵OA=2,OD=$\frac{3}{2}$,AD=$\frac{5}{2}$,PE=6,
∴PG=$\frac{24}{5}$,EG=$\frac{18}{5}$,
∵∠HPF=∠EPG,∠PFH=∠PGE,
∴△PFH∽△PGE,
∴$\frac{PH}{PE}$=$\frac{PF}{PG}$=$\frac{FH}{GE}$,
∴PF=3,FH=$\frac{9}{4}$,
∴S四边形GEFH=S△PGE-S△PFH=$\frac{1}{2}$×$\frac{24}{5}$×$\frac{18}{5}$-$\frac{1}{2}$×3×$\frac{9}{4}$=$\frac{1053}{200}$.
(3)如图2中,作QH⊥AD于H,旋转后H的对应点为H′.设M点坐标(m,$\frac{3}{4}$m+$\frac{3}{2}$).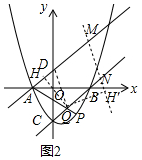
∵四边形QDMN是平行四边形,
∴DQ∥MN,DM∥QN,
∴∠QDH=∠DMN=∠QNH′,∵∠QHD=∠QH′N=90°,QH=QH′,
∴△QHD≌△QH′N,
∴DQ=QN,
∴四边形QDMN是菱形,
∴DQ=DM,
∵直线AP解析式为y=-$\frac{3}{4}$x-$\frac{3}{2}$,直线CN的解析式为y=$\frac{3}{4}$x-3,
由$\left\{\begin{array}{l}{y=-\frac{3}{4}x-\frac{3}{2}}\\{y=\frac{3}{4}x-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=-\frac{9}{4}}\end{array}\right.$,
∴点Q坐标(1,-$\frac{9}{4}$),
∵DQ=DM,
∴12+($\frac{3}{2}$+$\frac{9}{4}$)2=m2+($\frac{3}{4}$m)2,
解得m=±$\frac{\sqrt{241}}{5}$,
∴点M的坐标为($\frac{\sqrt{241}}{5}$,$\frac{3\sqrt{241}}{20}$+$\frac{3}{2}$)或(-$\frac{\sqrt{241}}{5}$,-$\frac{3\sqrt{241}}{5}$+$\frac{3}{2}$).
点评 本题考查二次函数综合题、最值问题、相似三角形的判定和性质、平行四边形的性质、菱形的判定和性质、勾股定理等知识,解题的关键是灵活运用这些知识解决问题,学会构建二次函数解决最值问题、学会利用方程组求两个函数的交点坐标,题目比较难,属于中考压轴题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:填空题
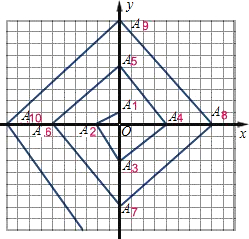 如图,在一单位长度为1cm的方格纸上,依如图所示的规律,设定点A1、A2、A3、A4、…An.连接点A1、A2、A3组成三角形,记为△1,面积S1=4;连接A2、A3、A4组成三角形,记为△2,面积S2=9;连接A3、A4、A5组成三角形,记为△3,面积S3=16…,连An、An+1、An+2组成三角形,记为△n(n为正整数),则面积Sn=(n+1)2.
如图,在一单位长度为1cm的方格纸上,依如图所示的规律,设定点A1、A2、A3、A4、…An.连接点A1、A2、A3组成三角形,记为△1,面积S1=4;连接A2、A3、A4组成三角形,记为△2,面积S2=9;连接A3、A4、A5组成三角形,记为△3,面积S3=16…,连An、An+1、An+2组成三角形,记为△n(n为正整数),则面积Sn=(n+1)2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com