
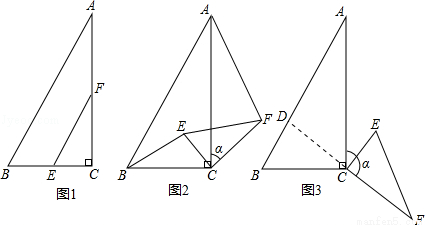
如图1,在△ABC中,∠ACB=90°,BC=2,∠A=30°,点E,F分别是线段BC,AC的中点,连结EF.
(1)线段BE与AF的位置关系是 ,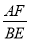 = .
= .
(2)如图2,当△CEF绕点C顺时针旋转a时(0°<a<180°),连结AF,BE,(1)中的结论是否仍然成立.如果成立,请证明;如果不成立,请说明理由.
(3)如图3,当△CEF绕点C顺时针旋转a时(0°<a<180°),延长FC交AB于点D,如果AD=6-2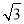 ,求旋转角a的度数.
,求旋转角a的度数.
(1) 线段BE与AF的位置关系是互相垂直; ;(2) (1)中结论仍然成立.证明见解析;(3)135°.
;(2) (1)中结论仍然成立.证明见解析;(3)135°.
【解析】
试题分析:(1)结合已知角度以及利用锐角三角函数关系求出AB的长,进而得出答案;
(2)利用已知得出△BEC∽△AFC,进而得出∠1=∠2,即可得出答案;
(3)过点D作DH⊥BC于H,则DB=4-(6-2 )=2
)=2 -2,进而得出BH=
-2,进而得出BH= -1,DH=3-
-1,DH=3- ,求出CH=BH,得出∠DCA=45°,进而得出答案.
,求出CH=BH,得出∠DCA=45°,进而得出答案.
试题解析:(1)如图1,线段BE与AF的位置关系是互相垂直;

∵∠ACB=90°,BC=2,∠A=30°,
∴AC=2 ,
,
∵点E,F分别是线段BC,AC的中点,
∴ =
= ;
;
(2)(1)中结论仍然成立.
证明:如图2,∵点E,F分别是线段BC,AC的中点,

∴EC= BC,FC=
BC,FC= AC,
AC,
∴ ,
,
∵∠BCE=∠ACF=α,
∴△BEC∽△AFC,
∴ ,
,
∴∠1=∠2,
延长BE交AC于点O,交AF于点M
∵∠BOC=∠AOM,∠1=∠2
∴∠BCO=∠AMO=90°
∴BE⊥AF;
(3)如图3,

∵∠ACB=90°,BC=2,∠A=30°
∴AB=4,∠B=60°
过点D作DH⊥BC于H
∴DB=4-(6-2 )=2
)=2 -2,
-2,
∴BH= -1,DH=3-
-1,DH=3- ,
,
又∵CH=2-( -1)=3-
-1)=3- ,
,
∴CH=BH,
∴∠HCD=45°,
∴∠DCA=45°,
∴α=180°-45°=135°.
考点:几何变换综合题.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源:2013-2014学年北京市昌平区中考一模数学试卷(解析版) 题型:选择题
抽奖箱里有6个除颜色外其他都相同的U盘,其中1个红色,2个黄色,3个蓝色,摇匀后从中任意摸出一个是黄色的概率为( )
A.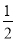 B.
B.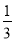 C.
C.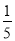 D.
D.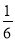
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市大兴区中考一模数学试卷(解析版) 题型:选择题
若菱形两条对角线的长分别为10cm和24cm,则这个菱形的周长为( )
A.13cm B.26cm C.34cm D.52cm
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市丰台区中考二模数学卷(解析版) 题型:解答题
如图,在四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=4,AD=6,求AC的长.
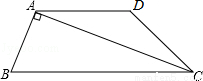
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市丰台区中考二模数学卷(解析版) 题型:填空题
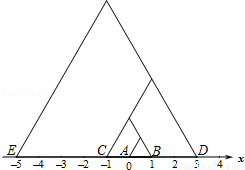
在数轴上,从原点A开始,以AB=1为边长画等边三角形,记为第一个等边三角形;以BC=2为边长画等边三角形,记为第二个等边三角形;以CD=4为边长画等边三角形,记为第三个等边三角形;以DE=8为边长画等边三角形,记为第四个等边三角形;…按此规律,继续画等边三角形,那么第五个等边三角形的面积是 ,第n个等边三角形的面积是
查看答案和解析>>
科目:初中数学 来源:2013-2014学年内蒙古满洲里市九年级三月月考数学试卷(解析版) 题型:填空题
如图,已知AD是△ABC的角平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,需添加一个条件是:___________,并给予证明.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年内蒙古九年级6月中考模拟数学试卷(解析版) 题型:选择题
点A(-3,4)与点B(m,n)关于x轴对称,则点B的坐标为
A.(-3, -4) B.(-3, 4) C.(3, -4) D.(3,4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com