
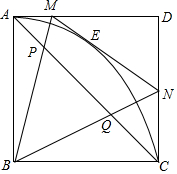
 已知,在边长为4的正方形ABCD中,以AB为半径作扇形AOC,E是弧AC上一动点,过E作弧AC的切线分别交AD,CD于点M和N.
已知,在边长为4的正方形ABCD中,以AB为半径作扇形AOC,E是弧AC上一动点,过E作弧AC的切线分别交AD,CD于点M和N.分析 (1)如图1,连接BE,根据切线的性质证明Rt△ABM≌Rt△EBM,则∠ABM=∠EBM,同理得:∠EBN=∠CBN,可得∠MBN=45°;
(2)如图2,将△ABM绕点B顺时针旋转90°得到△CBM′先表示S五边形MABCN=S△ABM+S△BMN+S△CBN=4MN,当4MN最小时,S△DMN最大,再由△DMN的周长为8,设DM=a,DN=b,由勾股定理得:MN=$\sqrt{{a}^{2}+{b}^{2}}$,计算当a=b时,MN有最小值是8($\sqrt{2}$-1),此时S△DMN最大,根据S△DMN=S正方形ABCD-S五边形MABCN求出最大值即可;
(3)如图1,证明△AMP∽CBP,列比例式$\frac{AM}{CB}=\frac{PM}{PB}$=$\frac{x}{4}$,由比例式的性质得:$\frac{BM}{PB}=\frac{x+4}{4}$,则PB=$\frac{4BM}{x+4}$,同理得:PC=$\frac{4AC}{x+4}$,再证明△BPQ∽△CPB,得:PB2=PQ•PC,可得y关于x的函数解析式.
解答 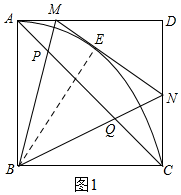 解:(1)如图1,连接BE,
解:(1)如图1,连接BE,
∵MN与⊙B相切,
∴BE⊥MN,
∴∠BEM=90°,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠BAD=∠BEM=90°,
∵AB=BE,BM=BM,
∴Rt△ABM≌Rt△EBM(HL),
∴∠ABM=∠EBM,
同理得:∠EBN=∠CBN,
∴∠EBM+∠EBN=∠ABM+∠CBN,
即∠MBN=∠ABM+∠CBN=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×90°=45°;
(2)如图2,将△ABM绕点B顺时针旋转90°得到△CBM′,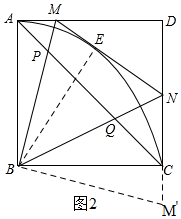
∴AM=CM′,BM=BM′,
∵∠BAM=∠BCD=∠BCM′=90°,
∴M′、C、D三点共线,
易证明△BMN≌△BM′N,
∴MN=NM′,
由(1)得:AM=ME,CN=EN,
∵S五边形MABCN=S△ABM+S△BMN+S△CBN=$\frac{1}{2}$AB•AM+$\frac{1}{2}$MN•BE+$\frac{1}{2}$BC•CN=$\frac{1}{2}$AB•2MN=$\frac{1}{2}$×4×2MN=4MN,
当4MN最小时,S△DMN最大,
△DMN中,DM+DN+MN=DM+EM+EN+DN=AD+DC=8,
设DM=a,DN=b,
∴MN=$\sqrt{{a}^{2}+{b}^{2}}$,
∵DM+DN+MN=8,
∴a+b+$\sqrt{{a}^{2}+{b}^{2}}$=8,
8=$\sqrt{(a+b)^{2}}$+$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{a}^{2}+{b}^{2}+2ab}$+$\sqrt{{a}^{2}+{b}^{2}}$≤$\sqrt{2({a}^{2}+{b}^{2})}$+$\sqrt{{a}^{2}+{b}^{2}}$=($\sqrt{2}$+1)$\sqrt{{a}^{2}+{b}^{2}}$=($\sqrt{2}$+1)MN,
∴MN≥$\frac{8}{\sqrt{2}+1}$=8($\sqrt{2}$-1),
当a=b时,MN有最小值是8($\sqrt{2}$-1),此时S△DMN最大,△DMN是等腰直角三角形,
此时,S△DMN=S正方形ABCD-S五边形MABCN=42-4MN=16-4×8($\sqrt{2}$-1)=48-32$\sqrt{2}$;
(3)如图1,∵AM∥BC,
∴△AMP∽CBP,
∴$\frac{AM}{CB}=\frac{PM}{PB}$=$\frac{x}{4}$,
∴$\frac{BM}{PB}=\frac{x+4}{4}$,
∴PB=$\frac{4BM}{x+4}$,
同理得:PC=$\frac{4AC}{x+4}$,
∵AC=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
∴PC=$\frac{4×4\sqrt{2}}{x+4}$=$\frac{16\sqrt{2}}{x+4}$,
∵∠PBQ=∠PCB=45°,∠BPQ=∠CPB,
∴△BPQ∽△CPB,
∴PB2=PQ•PC,
∴PQ=$\frac{P{B}^{2}}{PC}$=$\frac{(\frac{4BM}{x+4})^{2}}{\frac{16\sqrt{2}}{x+4}}$=$\frac{\sqrt{2}B{M}^{2}}{2(4+x)}$=$\frac{\sqrt{2}({x}^{2}+{4}^{2})}{2(4+x)}$=$\frac{\sqrt{2}({x}^{2}+16)}{8+2x}$;
即y=$\frac{\sqrt{2}({x}^{2}+16)}{8+2x}$.
点评 本题是圆的综合题,考查了圆的切线的性质、正方形的性质、旋转的性质、三角形全等和相似的性质和判定、勾股定理等知识,本题有难度,尤其是第二问,与比例的性质相结合,利用五边形面积的最小值得到△DMN面积的最大值.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:选择题
| A. | 平均数和众数都是3 | B. | 中位数为3 | ||
| C. | 方差为10 | D. | 标准差是$\frac{{\sqrt{15}}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
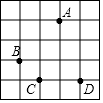 如图,每个小正方形的边长都是1,图中A,B,C,D四个点分别为小正方形的顶点,下列说法:
如图,每个小正方形的边长都是1,图中A,B,C,D四个点分别为小正方形的顶点,下列说法:| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com