
分析 设圆的半径为R,利用扇形面积公式得到圆心角为60°的扇形的面积=$\frac{1}{6}$πR2,加上圆的面积为πR2,于是得到扇形的面积占圆面积的$\frac{1}{6}$.
解答 解:设圆的半径为R,
圆心角为60°的扇形的面积=$\frac{60•π•{R}^{2}}{360}$=$\frac{1}{6}$πR2,
而圆的面积为πR2,
所以扇形的面积占圆面积的$\frac{1}{6}$.
故答案为:$\frac{1}{6}$.
点评 本题考查了扇形面积的计算:设圆心角是n°,圆的半径为R的扇形面积为S,则S扇形=$\frac{n•π•{R}^{2}}{360}$或S扇形$\frac{1}{2}$lR(其中l为扇形的弧长);求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.也考查了矩形的性质.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
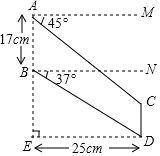 “C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)
“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com