练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    将正比例函数y=2x的图象沿y轴平移后，恰好经过点A（2，3），求平移后的函数解析式．
    考点：一次函数图象与几何变换
    专题：
    分析：正比例函数y=kx的图象沿y轴平移后，k的值不变．
    解答：解：设平移后直线方程为：y=2x+b．
    ∵正比例函数y=2x的图象沿y轴平移后，恰好经过点A（2，3），
    ∴3=4+b，
    解得 b=-1，
    则平移后的函数解析式为：y=2x-1．
    点评：本题考查了一次函数图象与几何变换．直线y=kx+b（k≠0，且k，b为常数）平移后，k保持不变，b发生变化．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    若代数式（x+a）（x-
    1
    2
    ）的结果中不含字母x的一次项，那么a的值是（　　）
    A、0
    B、2
    C、
    1
    2
    D、-
    1
    2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    一列快车从甲地匀速驶乙地，一列慢车从乙地匀速驶往甲地，慢车先发车半小时．设先发车辆行驶的时间为x/h，两车之间的距离为y/km，图中的折线表示y与x之间的函数关系，根据图象解决以下问题：
    （1）慢车的速度为
     
    km/h，快车的速度为
     
    km/h；
    （2）解释图中点C的实际意义
     
    ，解释图中点D的实际意义
     
    ；
    （3）直接写出点D的坐标
     
    ；点E的坐标
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

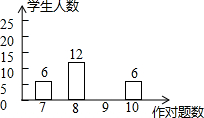    数学老师布置10道选择题当堂测试，统计结果每人至少答对7道题，数学课代表对全班48名同学的答题情况绘制了条形统计图．
    （1）请你补全统计图；
    （2）若规定学生至少答对9道题为优秀，求这次测试的优秀率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

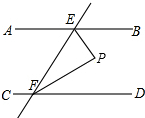    请将下列证明过程补充完整：
    已知：如图，AB∥CD，EF分别交AB、CD于点E、F，∠BEF的平分线与∠DFE的平分线相交于点P．
    求证：EP⊥FP．
    证明：因为AB∥CD（
     
    ）
    所以∠
     
    +∠DFE=180°（两直线平行，同旁内角互补）
    又因为EP平分∠BEF（已知）
    所以∠
     
    =
    1
    2
    ∠BEF（
     
    ）
    同理∠EFP=
    1
    2
    ∠DFE．
    所以∠PEF+∠EFP=
     
    °（等式性质）
    在△EFP中，
    因为∠PEF+∠EFP+∠P=180°（
     
    ）
    所以∠P=
     
    °
    所以EP⊥FP（
     
    ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在平面直角坐标系xOy中，直线y=kx+4（k≠0）与y轴交于点A．
    （1）如图，直线y=-2x+1与直线y=kx+4（k≠0）交于点B，与y轴交于点C，点B的横坐标为-1．
    ①求点B的坐标及k的值；
    ②直线y=-2x+1与直线y=kx+4与y轴所围成的△ABC的面积等于
     
    ；
    （2）直线y=kx+4（k≠0）与x轴交于点E（x0，0），若-2＜x0＜-1，求k的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

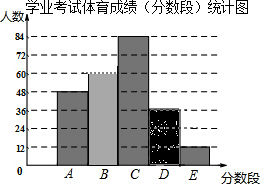    为了了解我市初四学生学业考试体育成绩，现从全市该年级学生中随机抽取了240名学生的体育成绩进行统计分段（A：100～90分；B：90～80分；C：80～70分；D：70～60分；E：60分以下）后，作出了频数分布直方图的一部分（每组数据含最大值，不含最小值）．请根据频数分布直方图，解答下列问题：
    （1）此次调查的总体是什么？
    （2）补全频数分布直方图；
    （3）如果把成绩在80分以上（不含80分）定为优秀，那么我市今年5100名初四学生中，体育成绩为优秀的学生约有多少名？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    平面内两条直线AB、CD互相平行，在两直线外取一点P（如图），

    （1）如图（1），请直接写出∠A，∠P，∠C之间存在的等量关系（不写理由）；
    （2）如图（2），写出∠A，∠P，∠C之间存在的等量关系，并说明理由；
    （3）如图（3），请直接写出∠A，∠P，∠C之间存在的等量关系（不写理由）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

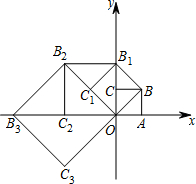    如图，在平面直角坐标系中有一个边长为1的正方形OABC，边OA，OC分别在x轴、y轴上，如果以对角线OB为边作第二个正方形OBB1C1，再以对角线OB1为边作第三个正方形OB1B2C2，…，照此规律作下去，则点B2的坐标为
     
    ；点B2014的坐标为
     
    ．

    查看答案和解析>>

    同步练习册答案