
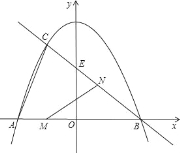
����Ŀ����ͼ��������y=![]() x2+3��x�ύ�ڵ�A����B����ֱ��y=
x2+3��x�ύ�ڵ�A����B����ֱ��y=![]() x+b�ཻ�ڵ�B����C��ֱ��y=
x+b�ཻ�ڵ�B����C��ֱ��y=![]() x+b��y�ύ�ڵ�E��
x+b��y�ύ�ڵ�E��
��1��д��ֱ��BC�Ľ���ʽ��
��2������ABC�������
��3������M���߶�AB����ÿ��1����λ���ȵ��ٶȴ�A��B�˶�������A��B�غϣ���ͬʱ����N������BC����ÿ��2����λ���ȵ��ٶȴ�B��C�˶������˶�ʱ��Ϊt�룬��д����MNB�����S��t�ĺ�����ϵʽ���������M�˶�����ʱ��ʱ����MNB���������������Ƕ��٣�
���𰸡���1��BC�Ľ���ʽΪy=![]() x+
x+![]() ��
��
��2��![]() ��4��
��4��![]() =
=![]()
��3������M�˶�2��ʱ����MNB������ﵽ������Ϊ![]() ��
��
��������
�����������1����y=0����y=-![]() x2+3�����A��B�����꣮��B���������y=-
x2+3�����A��B�����꣮��B���������y=-![]() x+b���BC�Ľ���ʽ��
x+b���BC�Ľ���ʽ��
��2���������������B��C�����꣮���AB��CD�ij�������������ABC�������
��3����N����NP��MB��֤����BNP�ס�BEO������֪��y=0�����E�����꣬�����߶α����NP��BE�ij������S��t�ĺ�����ϵʽ�����ö��κ������������S�����ֵ��
�����������1����y=-![]() x2+3����y=0����-
x2+3����y=0����-![]() x2+3=0����x1=2��x2=��2
x2+3=0����x1=2��x2=��2
��A����2��0����B��2��0�����ֵ�B��y=-![]() x+b�ϣ���0=-
x+b�ϣ���0=-![]() +b��b=
+b��b=![]()
��BC�Ľ���ʽΪy=-![]() x+
x+![]() ����
����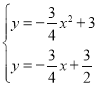 ����
����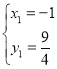 ��
��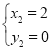 ��
��
��C(-1��![]() )��B��2��0������AB=4��CD=
)��B��2��0������AB=4��CD=![]() ��
��
��![]() ��4��
��4��![]() =
=![]() ������N��NP��MB�ڵ�P����EO��MB����NP��EO
������N��NP��MB�ڵ�P����EO��MB����NP��EO
���BNP�ס�BEO����![]() ����ֱ��y=-
����ֱ��y=-![]() x+
x+![]() �ɵã�E(0,
�ɵã�E(0,![]() )
)
������BEO��BO=2��EO=![]() ����BE=
����BE=![]() ����
����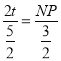 ����NP=
����NP=![]() t����S=
t����S=![]() .
.![]() t����4��t��=��
t����4��t��=��![]() t2+
t2+![]() t��0��t��4��=��
t��0��t��4��=��![]() ��t��2��2+
��t��2��2+![]()
���������߿������£�
����t=2ʱ��S���=![]() ��������M�˶�2��ʱ����MNB������ﵽ������Ϊ
��������M�˶�2��ʱ����MNB������ﵽ������Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Σ����Σ������ζ����е������ǣ� ��
A.ÿһ���Խ���ƽ��һ��Խ�
B.�Խ������
C.�Խ�����ƽ��
D.�Խ����ഹֱ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ж�����У����ܹ���������������ǣ� ��
A.��������
B.������
C.�������
D.��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ� ��
A.a5+a5=a10
B.a3a3=a9
C.��3a3��3=9a9
D.a12��a3=a9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ж����м�����ȷ���ǣ�������
A.aa2��a2B.��a2��3��a5C.��3xy��2��6x2y2D.a6��a2��a4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
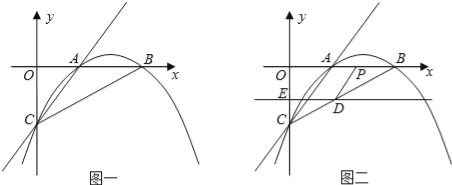
����Ŀ����֪����ͼһ��������y=ax2+bx+c��x�������ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��y=x��2����A��C���㣬��AB=2��
��1���������ߵĽ���ʽ��
��2����ֱ��DEƽ����x�Ტ��C�㿪ʼ��ÿ��1����λ���ٶ���y��������ƽ�ƣ��ҷֱ�y�ᡢ�߶�BC�ڵ�E��D��ͬʱ����P�ӵ�B��������BO������ÿ��2����λ�ٶ��˶�������ͼ2��������P�˶���ԭ��Oʱ��ֱ��DE���P��ֹͣ�˶�����DP������P�˶�ʱ��Ϊt�룻��s=![]() ����tΪ��ֵʱ��s����Сֵ���������Сֵ��
����tΪ��ֵʱ��s����Сֵ���������Сֵ��
��3���ڣ�2���������£��Ƿ����t��ֵ��ʹ��P��B��DΪ���������������ABC���ƣ������ڣ���t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com