
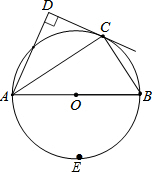
 如图,在四边形ABCD中,∠D=90°,AC平分∠DAB,且点C在以AB为直径的⊙O上.
如图,在四边形ABCD中,∠D=90°,AC平分∠DAB,且点C在以AB为直径的⊙O上.分析 (1)连接OC,如图1中.只要证明OC∥AD,由AD⊥CD,即可证明OC⊥CD解决问题.
(2)过点B作BF⊥CE于F,如图2中.①在Rt△ACB中,根据BC=AC•tan∠CAB,求出BC.②在Rt△CFB中,由∠BCF=42°及BC的长,可求CF,BF的长;③在Rt△EFB中,由∠E的三角函数值及BF的长,可EF的长;④由CE=CF+EF,可求CE的长.
解答 (1)证明:连接OC,如图1中.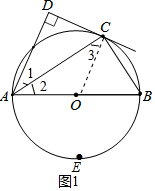
∵AC平分∠DAB,
∴∠1=∠2,
∵OA=OC,
∴∠3=∠2,
∴∠3=∠1,
∴AD∥OC,
∴∠OCD=∠D=90°,
又∵OC是⊙O的半径,
∴CD是⊙O的切线.
(2)求解思路如下:
过点B作BF⊥CE于F,如图.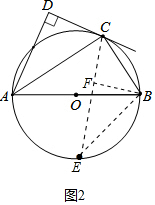
①在Rt△ACB中,根据BC=AC•tan∠CAB,求出BC.
②在Rt△CFB中,由∠BCF=42°及BC的长,可求CF,BF的长;
③在Rt△EFB中,由∠E的三角函数值及BF的长,可EF的长;
④由CE=CF+EF,可求CE的长.
点评 本题考查切线的判定、勾股定理、锐角三角函数、勾股定理等知识,解题的关键是学会添加常用辅助线,灵活运用锐角三角函数解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
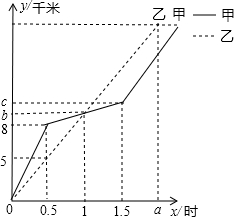 如图,表示甲、乙两人沿同一条路长跑,两人的行程y(千米)与时间x(时)变化的图象(全程)如图所示,根据图象回答问题:
如图,表示甲、乙两人沿同一条路长跑,两人的行程y(千米)与时间x(时)变化的图象(全程)如图所示,根据图象回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
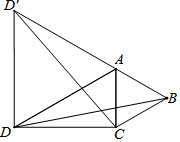 如图,在△ACD中,AD=9,CD=3$\sqrt{2}$,△ABC中,AB=AC.若∠CAB=60°,∠ADC=30°,在△ACD外作等边△ADD′
如图,在△ACD中,AD=9,CD=3$\sqrt{2}$,△ABC中,AB=AC.若∠CAB=60°,∠ADC=30°,在△ACD外作等边△ADD′查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
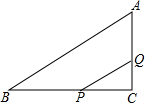 如图所示,在△ABC中,∠C=90°,BC=8厘米,AC=6厘米,点P从B点出发,以每秒2厘米的速度沿BC向C点移动;点Q从C点出发,以每秒1厘米的速度沿CA向A点移动.
如图所示,在△ABC中,∠C=90°,BC=8厘米,AC=6厘米,点P从B点出发,以每秒2厘米的速度沿BC向C点移动;点Q从C点出发,以每秒1厘米的速度沿CA向A点移动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com