
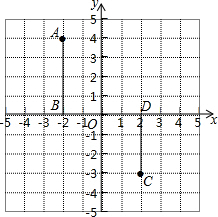
 如图,已知直角坐标系中四点A(-2,4)、B(-2,0)、C(2,-3)、D(2,0).若点P在x轴上,且PA、PB、AB所围成的三角形与PC、PD、CD所围成的三角形相似,则所有符合上述条件的点P的个数是( )
如图,已知直角坐标系中四点A(-2,4)、B(-2,0)、C(2,-3)、D(2,0).若点P在x轴上,且PA、PB、AB所围成的三角形与PC、PD、CD所围成的三角形相似,则所有符合上述条件的点P的个数是( )| A、1个 | B、2个 |
| C、3 个 | D、4个 |
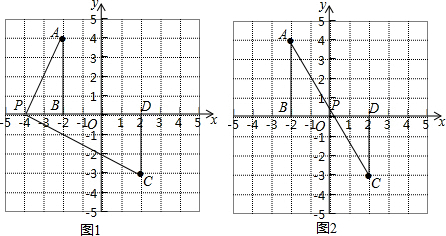 解:设OP=x(x>0),分三种情况:
解:设OP=x(x>0),分三种情况:| 2 |
| 7 |
| 2 |
| 7 |

| 2 |
| 7 |


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com