
 垂直的直线l,交x轴于P,
垂直的直线l,交x轴于P,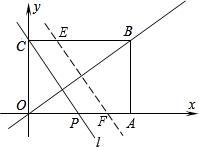
 ,
, x,
x, ,设直线l的解析式是y=-
,设直线l的解析式是y=- x+b,
x+b, x+6,设y=0,解得:x=
x+6,设y=0,解得:x= ,则P的坐标是(
,则P的坐标是( ,0);
,0); 时:
时: -x=
-x= ,设直线l与BC的交点是E,则BE=8-x,四边形ABEP是直角梯形,
,设直线l与BC的交点是E,则BE=8-x,四边形ABEP是直角梯形, (AP+BE)•AB=
(AP+BE)•AB= (
( +8-x)×6=-6x+
+8-x)×6=-6x+ ;
;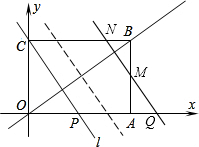
 <x≤8时,设直线l与AB交于点M,与BC交于点N.交x轴与Q.
<x≤8时,设直线l与AB交于点M,与BC交于点N.交x轴与Q. ,
, ,则AM=
,则AM=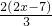 ,BM=6-
,BM=6-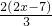 =
=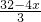 ,
, BN•BM=
BN•BM= x×
x×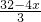 =
=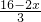 .
.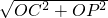 =
= ,
, +x,
+x, x,则M的坐标是:(
x,则M的坐标是:( +x,
+x, x),
x), x=1,解得:x=
x=1,解得:x= ;
; +x=1,解得:x=-
+x=1,解得:x=- ,(舍去);
,(舍去); +x)=1或(
+x)=1或( +x)-8=1,解得:x=
+x)-8=1,解得:x= 或
或 ;
; x=1或
x=1或 x-6=1,解得:x=
x-6=1,解得:x= 或
或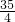 .
. 或当
或当 <x≤8以及x>8三种情况进行讨论,分别利用直角梯形的面积公式,以及直角三角形的面积公式即可求得函数解析式;
<x≤8以及x>8三种情况进行讨论,分别利用直角梯形的面积公式,以及直角三角形的面积公式即可求得函数解析式;

科目:初中数学 来源: 题型:
 如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
| 13 |
| 4 |

查看答案和解析>>
科目:初中数学 来源: 题型:
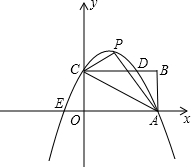 已知如图,矩形OABC的长OA=
已知如图,矩形OABC的长OA=| 3 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•樊城区模拟)已知如图,矩形OABC的长OA=2
(2013•樊城区模拟)已知如图,矩形OABC的长OA=2| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com