
| 环数 | 6 | 7 | 8 | 9 |
| 人数 | 1 | 5 | 3 | 1 |
分析 (1)根据众数的定义即一组数据中出现次数最多的数,即可得出答案;
(2)根据平均数的计算公式进行计算即可;
(3)用1200乘以优秀选手所占的百分比即可得出答案.
解答 解:(1)∵射击7环数的人数有5个,人数最多,
∴该小组射击数据的众数是7;
故答案为:7;
(2)该小组的平均成绩为:$\frac{1}{10}$(6+7×5+8×3+9)=7.4(环);
(3)根据题意得:
1200×$\frac{4}{10}$=480(人),
答:在1200名新生中有480人可以评为优秀射手.
点评 此题考查了众数、平均数和用样本估计总体,掌握众数的定义、用样本估计总体和平均数的计算公式是本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
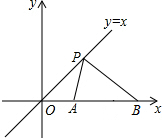 在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(2,0),B(6,0)是x轴上的两点,则PA+PB的最小值为2$\sqrt{10}$.
在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(2,0),B(6,0)是x轴上的两点,则PA+PB的最小值为2$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com