
 x2+h过点F,求此抛物线的解析式,并判断它与直线AD的交点的个数.
x2+h过点F,求此抛物线的解析式,并判断它与直线AD的交点的个数.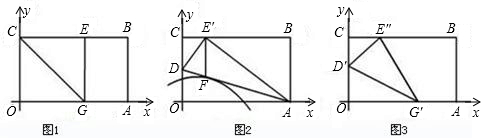
 =8,
=8, .
. )
) ,
, ,
, x+
x+ .
. ×2+
×2+ =
= ,
, ).
). x2+h上,
x2+h上, =-
=- ×4+h,
×4+h, x2+3.
x2+3. x2+
x2+ x-
x- =0,
=0, )2-4×(-
)2-4×(- )×(-
)×(- )=0
)=0 x2+3只有一个交点;
x2+3只有一个交点; x2+3上.
x2+3上. x2+3,
x2+3, x2+x-3=0.
x2+x-3=0. )=0,
)=0, x2+3只有一个交点.
x2+3只有一个交点. x2+3=-
x2+3=- ×62+3=0,
×62+3=0,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
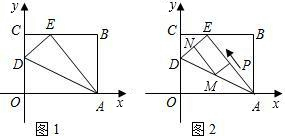
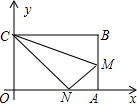 如图,四边形OABC是一张放在平面直角坐标系的矩形纸片,O为原点,点A在x轴上,点C在y轴上,OA=15,OC=9,在AB上取一点M,使得△CBM沿CM翻折后,点B落在x轴上,记作N点.
如图,四边形OABC是一张放在平面直角坐标系的矩形纸片,O为原点,点A在x轴上,点C在y轴上,OA=15,OC=9,在AB上取一点M,使得△CBM沿CM翻折后,点B落在x轴上,记作N点.查看答案和解析>>
科目:初中数学 来源: 题型:
 OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=6.
OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=6.查看答案和解析>>
科目:初中数学 来源: 题型:
 的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.
的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,则D点的坐标是
如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,则D点的坐标是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com