
| 板房型号 | 甲种板材 | 乙种板材 | 安置人数 |
| A型板房 | 54m2 | 26m2 | 6 |
| B型板房 | 78m2 | 41m2 | 9 |
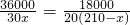



 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
| 板房型号 | 甲种板材 | 乙种板材 | 安置人数 |
| A型板房 | 54m2 | 26m2 | 6 |
| B型板房 | 78m2 | 41m2 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题10分)在灾民安置工作中,某企业接到一批生产甲种板材36000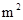 和乙种板材18000
和乙种板材18000![]() 的任务.
的任务.
(1)已知该企业安排210人生产这两种板材,每人每天能生产甲种板材30![]() 或乙种板材20
或乙种板材20![]() .问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
.问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
(2)某灾民安置点计划用该企业生产的这批板材搭建![]() 两种型号的板房共600间,在搭建过程中,按实际需要调运这两种板材.已知建一间
两种型号的板房共600间,在搭建过程中,按实际需要调运这两种板材.已知建一间![]() 型板房和一间
型板房和一间![]() 型板房所需板材及能安置的人数如下表所示:
型板房所需板材及能安置的人数如下表所示:
| 板房型号 | 甲种板材 | 乙种板材 | 安置人数 |
|
| 54 | 26 | 6 |
|
| 78 | 41 | 9 |
问:这600间板房最多能安置多少灾民?
查看答案和解析>>
科目:初中数学 来源: 题型:
 和乙种板材18000
和乙种板材18000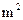 的任务.
的任务.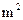 或乙种板材20
或乙种板材20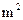 .问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
.问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?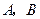 两种型号的板房共600间,在搭建过程中,按实际需要调运这两种板材.已知建一间
两种型号的板房共600间,在搭建过程中,按实际需要调运这两种板材.已知建一间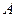 型板房和一间
型板房和一间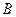 型板房所需板材及能安置的人数如下表所示:
型板房所需板材及能安置的人数如下表所示:| 板房型号 | 甲种板材 | 乙种板材 | 安置人数 |
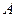 型板房 型板房 | 54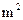 | 26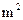 | 6 |
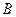 型板房 型板房 | 78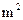 | 41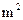 | 9 |
查看答案和解析>>
科目:初中数学 来源:北京市房山区2011年九年级学题统一练习 题型:解答题
(本题10分)在灾民安置工作中,某企业接到一批生产甲种板材36000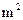 和乙种板材18000
和乙种板材18000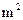 的任务.
的任务.
(1)已知该企业安排210人 生产这两种板材,每人每天能生产甲种板材30
生产这两种板材,每人每天能生产甲种板材30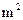 或乙种板材20
或乙种板材20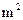 .问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
.问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
(2)某灾民安置点计划用该企业生产的这批板材搭建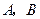 两种型号的板房共600间,在搭建过程中,按实际需要调运这两种板材.已知建一间
两种型号的板房共600间,在搭建过程中,按实际需要调运这两种板材.已知建一间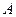 型板
型板 房和一间
房和一间 型板房所需板材及能安置的人数如下表所示:
型板房所需板材及能安置的人数如下表所示:
| 板房型号 | 甲种板材 | 乙种板材 | 安置人数 |
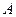 型板房 型板房 | 54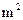 | 26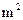 | 6 |
 型板房 型板房 | 78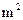 | 41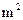 | 9 |
查看答案和解析>>
科目:初中数学 来源:2012届度河北北城中学初三第一学期期末数学试卷 题型:解答题
在灾民安置工作中,某企业接到一批生产甲种板材36000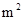 和乙种板材18000
和乙种板材18000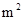 的任务.
的任务.
1.已知该企业安排210人生产这两种板材,每人每天能生产甲种板材30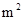 或乙种板材20
或乙种板材20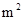 .问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
.问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
2.某灾民安置点计划用该企业生产的这批板材搭建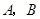 两种型号的板房共600间,在搭建过程中,按实际需要调运这两种板材.已知建一间
两种型号的板房共600间,在搭建过程中,按实际需要调运这两种板材.已知建一间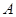 型板房和一间
型板房和一间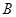 型板房所需板材及能安置的人数如下表所示
型板房所需板材及能安置的人数如下表所示
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com