
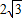 ,点E在AB的延长线上,且
,点E在AB的延长线上,且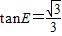 .
.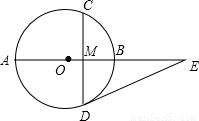
 ,可求出∠E,那么在△DOE中,利用三角形内角和等于180°可求出∠ODE=90°,从而DE是⊙O的切线;
,可求出∠E,那么在△DOE中,利用三角形内角和等于180°可求出∠ODE=90°,从而DE是⊙O的切线; ,在Rt△ODM中,OM=1,则AM=3,在Rt△ACM中,利用勾股定理可求AC=2
,在Rt△ODM中,OM=1,则AM=3,在Rt△ACM中,利用勾股定理可求AC=2 ,于是AC=DE=D′E′,根据题意,由平移到性质可知△ODE≌△O′AC,那么∠O′CA=30°,∠AOF=60°,再由平移的性质可知CF∥OA,在RT△FCD中,易求CF=2,∠CFO=∠FOC=60°,因此△FOC是等边三角形,于是CF=OA=2,因而S△AFO=S△AFC,那么重合部分的面积=S扇形AOF=
,于是AC=DE=D′E′,根据题意,由平移到性质可知△ODE≌△O′AC,那么∠O′CA=30°,∠AOF=60°,再由平移的性质可知CF∥OA,在RT△FCD中,易求CF=2,∠CFO=∠FOC=60°,因此△FOC是等边三角形,于是CF=OA=2,因而S△AFO=S△AFC,那么重合部分的面积=S扇形AOF= π.
π. (1)证明:连接OD.
(1)证明:连接OD. ,
, CD,
CD, =2.
=2. ,
, ,
, (2)解:∵∠ODE=90°,OD=2,∠E=30°,
(2)解:∵∠ODE=90°,OD=2,∠E=30°, ,
, ,
, .(5分)
.(5分)

科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2010年中考数学全真模拟试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2010年中考数学全真模拟试卷(解析版) 题型:解答题
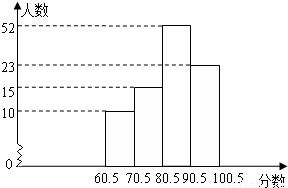
查看答案和解析>>
科目:初中数学 来源:2010年中考数学全真模拟试卷(解析版) 题型:选择题




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com