
如图,圆柱的底面半径为2cm,当圆柱的高由小到大变化时,圆柱的体积也发生了变化.

(1)在这个变化过程中,自变量是_______,因变量是________.
(2)如果圆柱的高为x(cm),圆柱的体积V(cm3)与x的关系式为_____.
(3)当圆柱的高由2cm变化到4cm时,圆柱的体积由_______cm3变化到_______cm3.
(4)当圆柱的高每增加1cm时,它的体积增加________cm3.
(1)圆柱的高,圆柱的体积;(2)V=4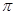 x;(3)8
x;(3)8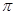 ,16
,16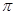 ;(4)4
;(4)4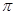
【解析】
试题分析:(1)根据常量和变量的定义来判断自变量、因变量和常量;
(2)根据圆柱的体积公式即可得到结果;
(3)根据圆柱的体积公式即可得到结果;
(4)根据圆柱的体积公式即可得到结果.
(1)在这个变化过程中,自变量是圆柱的高,因变量是圆柱的体积;
(2)圆柱的体积V(cm3)与x的关系式为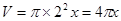 ;
;
(3)当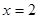 时,
时,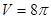 ,当
,当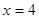 时,
时,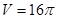 ,
,
则圆柱的体积由8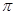 cm3变化到16
cm3变化到16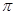 cm3;
cm3;
(4)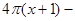
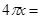
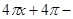
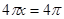 ,
,
则当圆柱的高每增加1cm时,它的体积增加4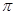 cm3.
cm3.
考点:本题主要考查变量的定义,圆柱的体积公式
点评:在一个变化的过程中,数值发生变化的量称为变量,函数值为因变量,另一个值为自变量.


科目:初中数学 来源: 题型:阅读理解
 | BC |


查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,圆柱的高是3cm,当圆柱的底面半径由小到大变化时,圆柱的体积也随之发生了变化.
如图,圆柱的高是3cm,当圆柱的底面半径由小到大变化时,圆柱的体积也随之发生了变化.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com