
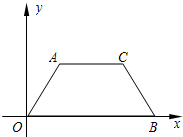
 标系xoy,已知已知A(2,2
标系xoy,已知已知A(2,2 ),B(8,0).
),B(8,0). );
); .
.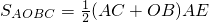 =
=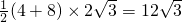 ;
;
 OB=4=AC.
OB=4=AC. OB.
OB. .
. );
);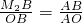 .
. .
. .
. ).
).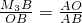 .
. .
. ).
). );由A、B、C的坐标与梯形面积的求解方法,可求得等腰梯形AOBC的面积;
);由A、B、C的坐标与梯形面积的求解方法,可求得等腰梯形AOBC的面积; OB,则可得点A在⊙D上;
OB,则可得点A在⊙D上; .
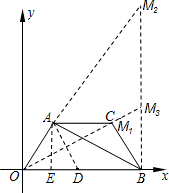
.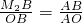 .当△OM3B与△BOA相似时,即过B点作OB的垂线交OC的延长线于M3(如图),则有
.当△OM3B与△BOA相似时,即过B点作OB的垂线交OC的延长线于M3(如图),则有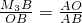 .代入数值依次求解即可.
.代入数值依次求解即可.

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
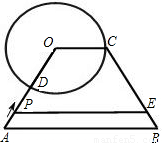
 A于点D,动点P以每秒1个单位的速度从点A沿AO向点O运动,过点P作PE∥AB交BC于点E.设P点运动的时间为t(秒).
A于点D,动点P以每秒1个单位的速度从点A沿AO向点O运动,过点P作PE∥AB交BC于点E.设P点运动的时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:
 (2009•上海模拟)已知:如图,在等腰梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,点E、F分别在线段OB、OC上,AO=OF,AE∥DF.
(2009•上海模拟)已知:如图,在等腰梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,点E、F分别在线段OB、OC上,AO=OF,AE∥DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 A于点D,动点P以每秒1个单位的速度从点A沿AO向点O运动,过点P作PE∥AB交BC于点E.设P点运动的时间为t(秒).
A于点D,动点P以每秒1个单位的速度从点A沿AO向点O运动,过点P作PE∥AB交BC于点E.设P点运动的时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在等腰梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,点E、F分别在线段OB、OC上,AO=OF,AE∥DF.
已知:如图,在等腰梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,点E、F分别在线段OB、OC上,AO=OF,AE∥DF.查看答案和解析>>
科目:初中数学 来源:2011年江苏省南京市浦口区中考数学二模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com