练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．如图，图1为一个长方体，AD=AB=10，AE=6，M，N为所在棱的中点．图2为图1的表面展开图．
    （1）在图2中，画出点M、N的位置，并连接MN；
    （2）求以图2中MM为边长的正方形面积．

    分析 运用勾股定理直接求出MN的长度，再根据正方形的面积公式即可解决问题．

    解答 解：图2中△MFN为直角三角形，
    由题意得：MF=NF=6+5=11，
    由勾股定理得MN=$\sqrt{1{1}^{2}+1{1}^{2}}$=11$\sqrt{2}$，
    11$\sqrt{2}$×11$\sqrt{2}$=242．
    故MM为边长的正方形面积为242．

    点评 主要考查了几何体的展开图、勾股定理的应用等问题；解题的关键是灵活运用勾股定理来分析、判断、解答．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

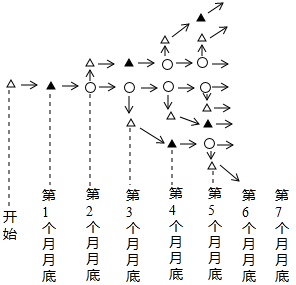    13．如果用△表示一对新出生的小兔，用▲表示一对一个月大的成年兔子，用○表示一对能生小兔的成年兔子，请你在图中标出第6个月月底和第7个月月底的各对兔子，把这幅图补充完整．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

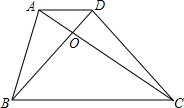    14．已知：在梯形ABCD中，AD∥BC．
    （1）求证：S△AOB=S△COD；
    （2）求证：S△AOB是S△AOD和S△BOC的比例中项；
    （3）求证：$\frac{AO}{AC}$=$\frac{DO}{DB}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．解下列方程：
    （1）（2x+3）2=x2-6x+9；                 
    （2）x2-5x+2=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

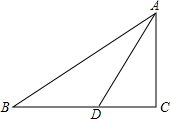    18．如图，在△ABC中，∠C=90°，AC=5cm，∠BAC的平分线交BC于D，AD=$\frac{10\sqrt{3}}{3}$cm，求∠B，AB，BC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

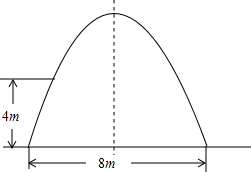    8．如图，某工厂大门是一抛物线型水泥建筑物，大门地面宽8m，大门高度9m，两侧距地面4m处各有一壁灯，则两壁灯之间水平距离（精确到0.1m，水泥厚度忽略不计）为（　　）
    A．6.0mB．5.3mC．5.6mD．5.9m

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．（1）如图①，△ABC是锐角三角形，高BD、CE相交于点H，找出∠BHC和∠A之间存在何种等量关系；
    （2）如图②，若△ABC是钝角三角形，∠A＞90°，高BD、CE所在的直线相交于点H，把图②补充完整，并指出此时（1）中的等量关系是否仍然成立？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．按如图程序计算，如果输入的数是-2，那么输出的数是-162．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．用长为100cm的金属丝制成一个长方形，当长方形各边长取多少时，长方形的面积是500cm2？要使长方形的面积为625cm2，其各边长应取多少？这段金属丝能制成面积为800cm2的矩形吗？

    查看答案和解析>>

    同步练习册答案