
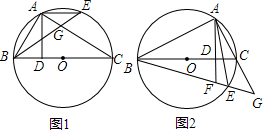
���� ��1�����ȸ���Բ�ܽǶ�������ֱ�Ķ���õ���BAD+��CAD=90�㣬��C+��CAD=90�㣬�Ӷ��õ���BAD=��C��Ȼ�����õȻ��ԵȽǵ�֪ʶ�õ�AF=BF���Ӷ�֤��FA=FG���ж����������Σ�
��2��������֤������ͬ��1����
��3�����ȸ�������õ�AF=BF=FG���Ӷ�������֪�����õ�FB=5��Ȼ�����ù��ɶ����õ�BD=4��DF=3���Ӷ����AD=2��������AB=2$\sqrt{5}$��
��� �⣺��1�����������Σ�
��BCΪֱ����AD��BC��
���BAD+��CAD=90�㣬��C+��CAD=90�㣬
���BAD=��C��
��$\widehat{AE}$=$\widehat{AB}$��
���ABE=��C��
���ABE=��BAD��
��AF=BF��
�ߡ�BAD+��CAD=90�㣬��ABE+��AGB=90�㣬
���DAC=��AGB��
��FA=FG��
���FAG�ǵ��������Σ�
��2��������
��BCΪֱ����AD��BC��
���BAD+��CAD=90�㣬��C+��CAD=90�㣬
���BAD=��C��
��$\widehat{AE}$=$\widehat{AB}$��
���ABE=��C��
���ABE=��BAD��
��AF=BF��
�ߡ�BAD+��CAD=90�㣬��ABE+��AGB=90�㣬
���DAC=��AGB��
��FA=FG��
���FAG�ǵ��������Σ�
��3���ɣ�2���ã�AF=BF=FG��
��BG=10��
��FB=5��
��$\left\{\begin{array}{l}{BD-DF=1}\\{B{D}^{2}+D{F}^{2}=25}\end{array}\right.$��
��ã�BD=4��DF=3��
��AD=2��
��AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=2$\sqrt{5}$��
���� ���⿼����Բ���ۺ�֪ʶ���������������ɶ�����֪ʶ������Ĺ�����ע����������ε��ж���Բ��֪ʶ�Ľ�ϣ��ѶȲ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6�� | B�� | 7�� | C�� | 8�� | D�� | 9�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2��5�� | B�� | ��2��-5�� | C�� | ��-2��5�� | D�� | ��-2��-5�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com