
【题目】如图,在平面直角坐标系中,在平面直角坐标系中,抛物线y=ax2+3x+c与x轴交于A、B两点,与y轴交于点C(0,8),直线l经过原点O,与抛物线的一个交点为D(6,8).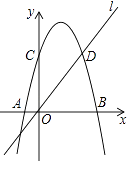
(1)求抛物线的解析式;
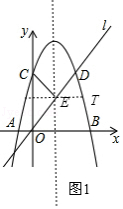
(2)抛物线的对称轴与直线l交于点E,点T为x轴上方的抛物线上的一个动点.
①当∠TEC=∠TEO时,求点T的坐标;
②直线BT与y轴交于点P,与直线l交于点Q,当OP=OQ时,求点P的坐标.
【答案】
(1)
解:把C、D两点的坐标代入抛物线解析式可得 ![]() ,解得
,解得 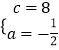 ,
,
∴抛物线解析式为y=﹣ ![]() x2+3x+8
x2+3x+8
(2)
解:①∵y=﹣ ![]() x2+3x+8=﹣
x2+3x+8=﹣ ![]() (x﹣3)2+
(x﹣3)2+ ![]() ,
,
∴抛物线对称轴为x=3,
设直线l解析式为y=kx,
把D(6,8)代入可得8=6k,解得k= ![]() ,
,
∴直线l的解析式为y= ![]() x,
x,
∴E(3,4),
∵O(0,0),C(0,8),
∴OE=CE,
∴点E在线段OC的垂直平分线上,
∵∠TEC=∠TEO,
∴TE∥x轴,
∴T的纵坐标为4,
在y=﹣ ![]() x2+3x+8中,令y=4可得4=﹣
x2+3x+8中,令y=4可得4=﹣ ![]() x2+3x+8,解得x=3+
x2+3x+8,解得x=3+ ![]() 或x=3﹣
或x=3﹣ ![]() ,
,
∴T的坐标为(3+ ![]() ,4)或(3﹣
,4)或(3﹣ ![]() ,4);
,4);
②在y=﹣ ![]() x2+3x+8中,令y=0可得0=﹣
x2+3x+8中,令y=0可得0=﹣ ![]() x2+3x+8,解得x=﹣2或x=8,
x2+3x+8,解得x=﹣2或x=8,
∴B(8,0),
∵E(3,4),
∴OE=5,
如图2,过点E作BP的平行线,交y轴于点F,交x轴于点H,
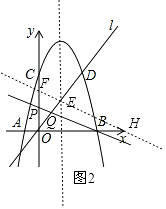
∴ ![]() =
= ![]() ,
,
∵OP=OQ,
∴OF=OE=5,
∴F(0,5),
∴可设直线PB的解析式为y=kx+5,
把E点坐标代入可得4=3k+5,解得k=﹣ ![]() ,
,
∴直线EF的解析式为y=﹣ ![]() x+5,
x+5,
∴可设直线PB的解析式为y=﹣ ![]() x+m,
x+m,
把B点坐标代入可得0=﹣ ![]() ×8+m,解得m=
×8+m,解得m= ![]() ,
,
∴P点坐标为(0, ![]() )
)
【解析】(1)由C、D坐标,利用待定系数法可求得抛物线解析式;(2)①可先求得抛物线的对称轴和直线l的解析式,则可求得E点坐标,由条件可证得TE∥x轴,则可求得T点纵坐标,代入抛物线解析式,可求得T点坐标;②过E作BP的平行线,交y轴于点F,交x轴于点H,利用平行线分线段成比例可求得OF=OE,可求得F点坐标,则可求得直线EF的解析式,则可设出直线PB的解析式,把B点代入可求得直线PB解析式,可求得P点坐标.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】为鼓励居民节约用水,某市对居民用水收费实行“阶梯水价”,按每年用水量统计,不超过180立方米的部分按每立方米5元收费;超过180立方米不超过260立方米的部分按每立方米7元收费;超过260立方米的部分按每立方米9元收费.
(1)设每年用水量为x立方米,按“阶梯水价”应缴水费y元,请写出y(元)与x(立方米)之间的函数解析式;
(2)明明家预计2015年全年用水量为200立方米,那么按“阶梯水价”收费,她家应缴水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
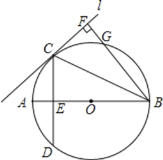
【题目】如图所示,已知AB是![]() 的直径,直线L与
的直径,直线L与![]() 相切于点C,
相切于点C,![]() ,CD交AB于E,
,CD交AB于E,![]() 直线L,垂足为F,BF交
直线L,垂足为F,BF交![]() 于C.
于C.
![]() 图中哪条线段与AE相等?试证明你的结论;
图中哪条线段与AE相等?试证明你的结论;
![]() 若
若![]() ,
,![]() ,求AB的值.
,求AB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2m+1)x+m(m+1)=0
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两根分别为x1、x2 , 求x ![]() +x
+x ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一食堂需要购买盒子存放食物,盒子有A、B两种型号,单个盒子的容量和价格如表格所示.现有15升食物需要存放且要求每个盒子都要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性每个返还现金1.5元,则该食堂购买盒子所需的最少费用是 .
型号 | A | B |
单个盒子容量(升) | 2 | 3 |
单价(元) | 5 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:某商场因换季,将一品牌服装打折销售,每件服装如果按标价的六折出售将亏10元,而按标价的七五折出售将赚50元,问:
(1) 每件服装的标价是多少元?
(2) 每件服装的成本是多少元?
(3)为保证不亏本,最多能打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线 ![]() (其中
(其中 ![]() )与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
(1)求抛物线的关系式;
(2)过点 ![]() 的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com