
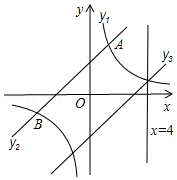
 如图所示,在同一直角坐标系xOy中,有双曲线y1=$\frac{{k}_{1}}{x}$,直线y2=k2x+b1,y3=k3x+b2,且点A(2,5),点B(-6,n)在双曲线的图象上
如图所示,在同一直角坐标系xOy中,有双曲线y1=$\frac{{k}_{1}}{x}$,直线y2=k2x+b1,y3=k3x+b2,且点A(2,5),点B(-6,n)在双曲线的图象上分析 (1)由点A可得反比例函数解析式,据此求得点B坐标,利用点A、B坐标可求得直线y2的解析式;
(2)由x=4与双曲线解析式求得交点C的坐标,由y3∥y2知k3=k2=$\frac{5}{6}$,结合点C坐标可得直线y3的解析式;
(3)利用函数图象找到双曲线位于直线y3下方所对应的x的范围即可.
解答 解:(1)把A(2,5)代入双曲线y1=$\frac{{k}_{1}}{x}$得k1=2×5=10,
∴y1=$\frac{10}{x}$,
把B(-6,n)代入y1=$\frac{10}{x}$得:-6n=10,
解得n=-$\frac{5}{3}$,
∴B点坐标为(-6,-$\frac{5}{3}$),
把A(2,5),B(-6,-$\frac{5}{3}$)代入y2=k2x+b1得$\left\{\begin{array}{l}{2{k}_{2}+{b}_{1}=5}\\{-6{k}_{2}+{b}_{1}=-\frac{5}{3}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{2}=\frac{5}{6}}\\{{b}_{1}=\frac{10}{3}}\end{array}\right.$,
∴y2=$\frac{5}{6}$x+$\frac{10}{3}$;
(2)如图,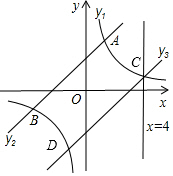
把x=4代入y1=$\frac{10}{x}$得y=$\frac{5}{2}$,
则C点坐标为(4,$\frac{5}{2}$),
∵y3∥y2,
∴k3=k2=$\frac{5}{6}$,
把C(4,$\frac{5}{2}$)代入y3=$\frac{5}{6}$x+b2得$\frac{5}{2}$=$\frac{5}{6}$×4+b2,
解得b2=-$\frac{5}{6}$,
∴y3=$\frac{5}{6}$x-$\frac{5}{6}$;
(3)-3<x<0或x>4.
点评 本题考查了反比例函数图象与一次函数图象的交点问题:反比例函数图象与一次函数图象的交点坐标同时满足两个函数解析式;利用待定系数法可求函数的解析式.也考查了观察图象的能力.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
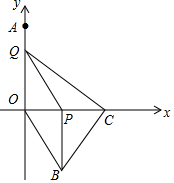 如图,在平面直角坐标系中,点A (0,4).动点P从原点O出发,沿x轴正方向以每秒2个单位的速度运动,同时动点Q从点A出发,沿y轴负方向以每秒1个单位的速度运动,以QO、QP为邻边构造平行四边形OQPB,在线段OP的延长线长取点C,使得PC=2,连接BC、CQ.设点P、Q运动的时间为t(0<t<4)秒.
如图,在平面直角坐标系中,点A (0,4).动点P从原点O出发,沿x轴正方向以每秒2个单位的速度运动,同时动点Q从点A出发,沿y轴负方向以每秒1个单位的速度运动,以QO、QP为邻边构造平行四边形OQPB,在线段OP的延长线长取点C,使得PC=2,连接BC、CQ.设点P、Q运动的时间为t(0<t<4)秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,利用热气球探测器测量大楼AB的高度,从热气球P处测得大楼B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离底面的高度为120m.试求大楼AB的高度(结果保留整数).
如图,利用热气球探测器测量大楼AB的高度,从热气球P处测得大楼B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离底面的高度为120m.试求大楼AB的高度(结果保留整数).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.393×107 | B. | 3.93×105 | C. | 3.93×106 | D. | 393×103 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
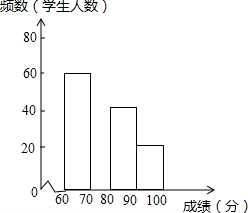 在2017迎新春汉字听写大会上,石家庄市中学生表现优秀,成绩都达到了60分(包含60分)以上,为了了解各个分数段的分布情况.随机抽取了200名学生的成绩进行统计(成绩都为整数,且满分是100分),经过整理,得到两幅不完整的统计图表(如图).
在2017迎新春汉字听写大会上,石家庄市中学生表现优秀,成绩都达到了60分(包含60分)以上,为了了解各个分数段的分布情况.随机抽取了200名学生的成绩进行统计(成绩都为整数,且满分是100分),经过整理,得到两幅不完整的统计图表(如图).| 成绩x(分) | 频数 | 频率 |
| 60≤x<70 | 60 | 0.30 |
| 70≤x<80 | m | 0.40 |
| 80≤x<90 | 40 | n |
| 90≤x<100 | 20 | 0.10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com