
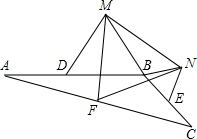
 点D、E、F分别是△ABC的边AB、BC、CA的中点.如图所示,若以BD、BE为边分别作正△BMD和正△BEN,连接MF、FN、MN. 易证△FMN是等边三角形,因而∠MFN=60°;若以BD、BE为边分别作正方形BPMD和正方形BQNE,连接MF、NF、MN,则∠MFN的度数是________;若以BD、BE为边分别作正n边形,设两个正n边形与点D、E相邻的顶点分别是M、N(点M、N与点B是不同的点),连接MF、NF、MN得到△FMN,则∠MFN的度数是________.
点D、E、F分别是△ABC的边AB、BC、CA的中点.如图所示,若以BD、BE为边分别作正△BMD和正△BEN,连接MF、FN、MN. 易证△FMN是等边三角形,因而∠MFN=60°;若以BD、BE为边分别作正方形BPMD和正方形BQNE,连接MF、NF、MN,则∠MFN的度数是________;若以BD、BE为边分别作正n边形,设两个正n边形与点D、E相邻的顶点分别是M、N(点M、N与点B是不同的点),连接MF、NF、MN得到△FMN,则∠MFN的度数是________.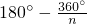

 AB,BE=CE=
AB,BE=CE= BC,
BC, BC,EF=
BC,EF= ,
,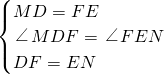 ,
,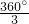 ,
, ,
, .
. .
.

科目:初中数学 来源: 题型:
 如图,小明家住16楼,楼前有一条河.小明在阳台距离地面50米的A点(AD=50m)分别看向河的两岸(B点和C点),测得俯角分别是45°与30°,请你求出河宽是多少?(精确到0.1米)
如图,小明家住16楼,楼前有一条河.小明在阳台距离地面50米的A点(AD=50m)分别看向河的两岸(B点和C点),测得俯角分别是45°与30°,请你求出河宽是多少?(精确到0.1米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com