
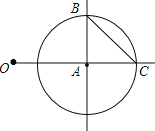
【题目】如图, ![]() ,以点A为圆心,1为半径画
,以点A为圆心,1为半径画![]() 与OA的延长线交于点C,过点A画OA的垂线,垂线与
与OA的延长线交于点C,过点A画OA的垂线,垂线与![]() 的一个交点为B,连接BC
的一个交点为B,连接BC
![]() 线段BC的长等于______;
线段BC的长等于______;
![]() 请在图中按下列要求逐一操作,并回答问题:
请在图中按下列要求逐一操作,并回答问题:
![]() 以点______为圆心,以线段______的长为半径画弧,与射线BA交于点D,使线段OD的长等于
以点______为圆心,以线段______的长为半径画弧,与射线BA交于点D,使线段OD的长等于![]()
![]() 连OD,在OD上画出点P,使OP的长等于
连OD,在OD上画出点P,使OP的长等于![]() ,请写出画法,并说明理由.
,请写出画法,并说明理由.
【答案】 ![]() A BC
A BC
【解析】分析:
(1)由题意易得∠BAC=90°,AC=AB=1,由此即可在Rt△ABC中由勾股定理解得BC的长;
(2)①由题意易得∠OAC=90°,结合OA=2,OD=![]() ,在Rt△OAD中解得AD=
,在Rt△OAD中解得AD=![]() =BC,由此即可得到本题各空的答案;②由题意可得:OA=2,OC=3,OP=
=BC,由此即可得到本题各空的答案;②由题意可得:OA=2,OC=3,OP=![]() ,OD=
,OD=![]() ,由此可得:OA:OC=OP:OD,从而可得AP∥CD,由此可知:只需过点A作CD的平行线AP交OD于点P即可.
,由此可得:OA:OC=OP:OD,从而可得AP∥CD,由此可知:只需过点A作CD的平行线AP交OD于点P即可.
详解:
(1)在![]() 中,
中, ![]() ,
,
∴![]() .
.
故答案为: ![]() .
.
(2)①在![]() 中,
中, ![]() ,
,
∴![]() .
.
∴以点A为圆心,以线段BC的长为半径画弧,与射线BA交于点D,即可使线段OD的长等于![]() .
.
依此画出图形,如图1所示.
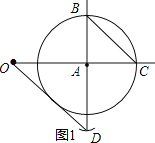
故答案为:A;BC.
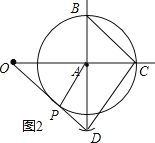
②∵![]() ,
,
∴![]() ,
,
∴![]() .
.
故作法如下:
连接CD,过点A作![]() 交OD于点
交OD于点![]() 点即是所要找的点.
点即是所要找的点.
依此画出图形,如图2所示.


科目:初中数学 来源: 题型:
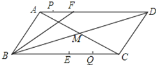
【题目】如图,![]() 中,点E是BC的中点,点F在AD上,AF=6cm,BF=12cm,BD平分∠FBC,若点P,Q分别是AF,BC上点,且CQ=2AP.若点P、Q、E、F为顶点的四边形构成平行四边形,则AP的长为______.
中,点E是BC的中点,点F在AD上,AF=6cm,BF=12cm,BD平分∠FBC,若点P,Q分别是AF,BC上点,且CQ=2AP.若点P、Q、E、F为顶点的四边形构成平行四边形,则AP的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆市的重大惠民工程--公租房建设已陆续竣工,计划10年内解决低收入人群的住房问题,前6年,每年竣工投入使用的公租房面积![]() 单位:百万平方米
单位:百万平方米![]() ,与时间x的关系是
,与时间x的关系是![]() 单位:年,
单位:年, ![]() 且x为整数
且x为整数![]() ;后4年,每年竣工投入使用的公租房面积
;后4年,每年竣工投入使用的公租房面积![]() 单位:百万平方米
单位:百万平方米![]() ,与时间x的关系是
,与时间x的关系是![]() 单位:年,
单位:年, ![]() 且x为整数
且x为整数![]() 假设每年的公租房全部出租完
假设每年的公租房全部出租完![]() 另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金
另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金![]() 单位:元
单位:元![]() 与时间
与时间![]() 单位:年,
单位:年, ![]() 且x为整数
且x为整数![]() 满足一次函数关系如下表:
满足一次函数关系如下表:
| 50 | 52 | 54 | 56 | 58 |
|
| 1 | 2 | 3 | 4 | 5 |
|
![]() 求出z与x的函数关系式;
求出z与x的函数关系式;
![]() 求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
![]() 若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高
若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高![]() ,这样可解决住房的人数将比第6年减少
,这样可解决住房的人数将比第6年减少![]() ,求a的值.
,求a的值.
![]() 参考数据:
参考数据: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买![]() 两种型号的垃圾处理设备共10台,已知每台
两种型号的垃圾处理设备共10台,已知每台![]() 型设备日处理能力为12吨;每台
型设备日处理能力为12吨;每台![]() 型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
(1)请你为该景区设计购买![]() 两种设备的方案;
两种设备的方案;
(2)已知每台![]() 型设备价格为3万元,每台
型设备价格为3万元,每台![]() 型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了全面提高学生的能力,学校组织课外活动小组,并要求初一学年积极参加,初一学年共有四个班,参加的学生共有(6a﹣3b)人,其中一班有a人参加,二班参加的人数比一班参加的人数两倍少b人,三班参加的人数比二班参加的人数一半多1人.
(1)求三班的人数(用含a,b的式子表示);
(2)求四班的人数(用含a,b的式子表示);
(3)若四个班共54人参加了课外活动,求二班比三班多多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某股民在上星期买进某种股票1000股,每股100元,下表是本周每日该股票的涨跌情况 (单位:元):

(1)该股在本周内最高价是每股多少元?最低价是每股多少元?
(2)星期三收盘时,每股是多少元?
(3)已知买进股票时需付成交额的1.5‰的手续费,卖出时需付成交额的1.5‰手续费和 1‰的交易费,如果在星期五收盘前将股票一次性卖出,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=(m﹣2)xm2+m-4 +2x﹣1是一个二次函数,求该二次函数的解析式.
【答案】y=﹣5x2+2x﹣1
【解析】试题分析:根据二次函数的定义得到m2+m﹣4=2且m﹣2≠0,由此求得m的值,进而得到该二次函数的解析式.
试题解析:依题意得:m2+m﹣4=2且m﹣2≠0. 即(m﹣2)(m+3)=0且m﹣2≠0,
解得m=﹣3,
则该二次函数的解析式为y=﹣5x2+2x﹣1
【题型】解答题
【结束】
21
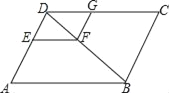
【题目】如图,在ABCD中,EF∥AB,FG∥ED,DE:DA=2:5,EF=4,求线段CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
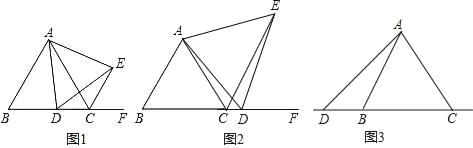
【题目】已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作等边△ADE(顶点A、D、E按逆时针方向排列),连接CE.
(1)如图1,当点D在边BC上时,求证:①BD=CE,②AC=CE+CD;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CE+CD是否成立?若不成立,请写出AC、CE、CD之间存在的数量关系,并说明理由;
(3)如图3,当点D在边BC的反向延长线上且其他条件不变时,补全图形,并直接写出AC、CE、CD之间存在的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.
(1)求篮球和足球的单价;
(2)根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的![]() ,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
(3)若购买篮球x个,学校购买这批篮球和足球的总费用为y(元),在(2)的条件下,求哪种方案能使y最小,并求出y的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com