
 如图,已知点C是
如图,已知点C是 的中点,半径OC与弦AB相交于D,如果∠OAB=60°,AB=8厘米,那么∠AOD=________度; CD=________厘米.
的中点,半径OC与弦AB相交于D,如果∠OAB=60°,AB=8厘米,那么∠AOD=________度; CD=________厘米.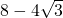
 ∠AOB=30°,所以通过解直角△AOD求得OD=4
∠AOB=30°,所以通过解直角△AOD求得OD=4 厘米,故CD=OC-OD=OA-OD=8-4
厘米,故CD=OC-OD=OA-OD=8-4 (厘米).
(厘米). 的中点,
的中点, ∠AOB=30°,AB⊥OC,
∠AOB=30°,AB⊥OC, (厘米)
(厘米) (厘米).
(厘米). .
.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源:2012-2013学年浙江萧山高桥、湘湖初中八年级上期中数学试卷(带解析) 题型:填空题
如图,已知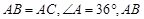 的中垂线
的中垂线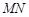 交
交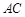 于点
于点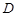 ,交
,交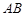 于点
于点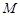 ,有下面4个结论:①射线
,有下面4个结论:①射线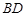 是
是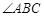 的角平分线;②图中共有三个等腰三角形;③
的角平分线;②图中共有三个等腰三角形;③ 的周长=AB+BC;④
的周长=AB+BC;④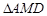 ≌
≌ 。
。
其中正确的有________。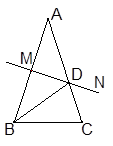
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江建德李家镇初级中学八年级5月单元检测数学试卷(带解析) 题型:解答题
如图,已知A,B两点是直线AB与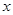 轴的正半轴,
轴的正半轴,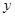 轴的正半轴的交点,且OA,OB的长分别是
轴的正半轴的交点,且OA,OB的长分别是 的两个根(OA>OB),射线BC平分∠ABO交
的两个根(OA>OB),射线BC平分∠ABO交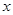 轴于C点,若有一动点P以每秒1个单位的速度从B点开始沿射线BC移动,运动时间为t秒.
轴于C点,若有一动点P以每秒1个单位的速度从B点开始沿射线BC移动,运动时间为t秒.
(1)设△APB和△OPB的面积分别为S1,S2,求S1∶S2;
(2)求直线BC的解析式;
(3)在点P的运动过程中,△OPB可能是等腰三角形吗?若可能,直接写出时间t的值,若不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆万州岩口复兴学校九年级上学期第三次月考数学试卷(解析版) 题型:解答题
如图,已知: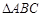 为边长是
为边长是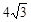 的等边三角形,四边形
的等边三角形,四边形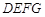 为边长是6的正方形. 现将等边
为边长是6的正方形. 现将等边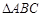 和正方形
和正方形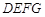 按如图①的方式摆放,使点
按如图①的方式摆放,使点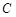 与点
与点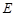 重合,点
重合,点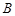 、
、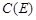 、
、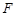 在同一条直线上,
在同一条直线上,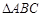 从图①的位置出发,以每秒1个单位长度的速度沿
从图①的位置出发,以每秒1个单位长度的速度沿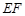 方向向右匀速运动,当点
方向向右匀速运动,当点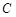 与点
与点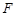 重合时暂停运动,设
重合时暂停运动,设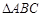 的运动时间为
的运动时间为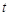 秒(
秒(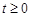 ).
).
(1)在整个运动过程中,设等边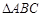 和正方形
和正方形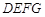 重叠部分的面积为
重叠部分的面积为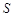 ,请直接写出
,请直接写出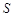 与
与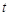 之间的函数关系式;
之间的函数关系式;
(2)如图②,当点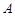 与点
与点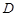 重合时,作
重合时,作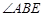 的角平分线
的角平分线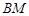 交
交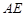 于点
于点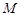 ,将
,将 绕点
绕点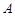 逆时针旋转,使边
逆时针旋转,使边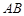 与边
与边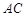 重合,得到
重合,得到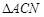 . 在线段
. 在线段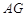 上是否存在
上是否存在 点,使得
点,使得 为等腰三角形. 如果存在,求线段
为等腰三角形. 如果存在,求线段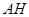 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
(3)如图③,若四边形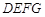 为边长是
为边长是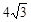 的正方形,
的正方形,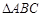 的移动速度为每秒
的移动速度为每秒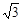 个单位长度,其余条件保持不变.
个单位长度,其余条件保持不变.
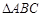 开始移动的同时,
开始移动的同时,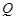 点从
点从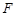 点开始,沿折线
点开始,沿折线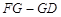 以每秒
以每秒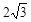 个单位长度开始移动,
个单位长度开始移动,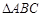 停止运动时,
停止运动时,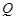 点也停止运动. 设在运动过程中,
点也停止运动. 设在运动过程中,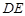 交折线
交折线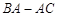 于
于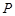 点,则当
点,则当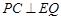 时,求
时,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年重庆市一中九年级(上)期末数学试卷(解析版) 题型:解答题
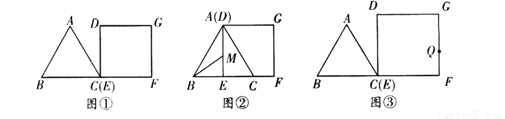
 的等边三角形,四边形DEFG为边长是6的正方形.现将等边△ABC和正方形DEFG按如图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,△ABC从图1的位置出发,以每秒1个单位长度的速度沿EF方向向右匀速运动,当点C与点F重合时暂停运动,设△ABC的运动时间为t秒(t≥0).
的等边三角形,四边形DEFG为边长是6的正方形.现将等边△ABC和正方形DEFG按如图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,△ABC从图1的位置出发,以每秒1个单位长度的速度沿EF方向向右匀速运动,当点C与点F重合时暂停运动,设△ABC的运动时间为t秒(t≥0).
 的正方形,△ABC的移动速度为每秒
的正方形,△ABC的移动速度为每秒 个单位长度,其余条件保持不变.△ABC开始移动的同时,Q点从F点开始,沿折线FG-GD以每秒
个单位长度,其余条件保持不变.△ABC开始移动的同时,Q点从F点开始,沿折线FG-GD以每秒 个单位长度开始移动,△ABC停止运动时,Q点也停止运动.设在运动过程中,DE交折线BA-AC于P点,则是否存在t的值,使得PC⊥EQ,若存在,请求出t的值;若不存在,请说明理由.
个单位长度开始移动,△ABC停止运动时,Q点也停止运动.设在运动过程中,DE交折线BA-AC于P点,则是否存在t的值,使得PC⊥EQ,若存在,请求出t的值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:2011-2012学年重庆市九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,已知:△ABC为边长是 的等边三角形,四边形DEFG为边长是6的正方形.现将等边△ABC和正方形DEFG按如图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,△ABC从图1的位置出发,以每秒1个单位长度的速度沿EF方向向右匀速运动,当点C与点F重合时暂停运动,设△ABC的运动时间为t秒(
的等边三角形,四边形DEFG为边长是6的正方形.现将等边△ABC和正方形DEFG按如图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,△ABC从图1的位置出发,以每秒1个单位长度的速度沿EF方向向右匀速运动,当点C与点F重合时暂停运动,设△ABC的运动时间为t秒(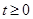 ).
).
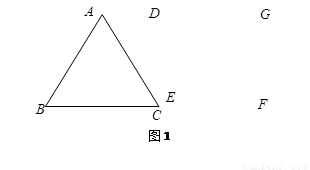
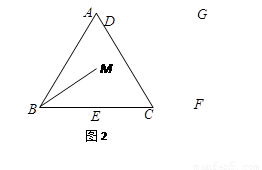
1.在整个运动过程中,设等边△ABC和正方形DEFG重叠部分的面积为S,请直接写出S与t之间的函数关系式;
2.如图2,当点A与点D重合时,作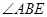 的角平分线EM交AE于M点,将△ABM绕点A逆时针旋转,使边AB与边AC重合,得到△ACN.在线段AG上是否存在H点,使得△ANH为等腰三角形.如果存在,请求出线段EH的长度;若不存在,请说明理由.
的角平分线EM交AE于M点,将△ABM绕点A逆时针旋转,使边AB与边AC重合,得到△ACN.在线段AG上是否存在H点,使得△ANH为等腰三角形.如果存在,请求出线段EH的长度;若不存在,请说明理由.
3.如图3,若四边形DEFG为边长为 的正方形,△ABC的移动速度为每秒
的正方形,△ABC的移动速度为每秒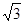 个单位长度,其余条件保持不变.△ABC开始移动的同时,Q点从F点开始,沿折线FG-GD以每秒
个单位长度,其余条件保持不变.△ABC开始移动的同时,Q点从F点开始,沿折线FG-GD以每秒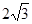 个单位长度开始移动,△ABC停止运动时,Q点也停止运动.设在运动过程中,DE交折线BA-AC于P点,则是否存在t的值,使得
个单位长度开始移动,△ABC停止运动时,Q点也停止运动.设在运动过程中,DE交折线BA-AC于P点,则是否存在t的值,使得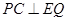 ,若存在,请求出t的值;若不存在,请说明理由
,若存在,请求出t的值;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com