y=-
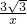
分析:连接AC,求出△BAC是等边三角形,推出AC=AB,求出△DC′B′是等边三角形,推出C′D=B′D,得出CB=BD=B′C′,推出A和D重合,连接BB′交x轴于E,求出AB′=AB=2,∠B′AE=60°,求出B′的坐标是(3,-

),设经过点B′反比例函数的解析式是y=

,代入求出即可.
解答:

连接AC,
∵四边形OABC是菱形,
∴CB=AB,∠CBA=∠AOC=60°,
∴△BAC是等边三角形,
∴AC=AB,
∵将四边形OABC沿直线0D翻折,使点B和点C分别落在这个坐标平面的点B′和C′处,
∴BD=B′D,CD=C′D,∠DB′C′=∠ABC=60°,
∵∠B′DC′=60°,
∴∠DC′B′=60°,
∴△DC′B′是等边三角形,
∴C′D=B′D,
∴CB=BD=B′C′,
即A和D重合,
连接BB′交x轴于E,
则AB′=AB=2,∠B′AE=180°-(180°-60°)=60°,
在Rt△AB′E中,∠B′AE=60°,AB′=2,
∴AE=1,B′E=

,OE=2+1=3,
即B′的坐标是(3,-

),
设经过点B′反比例函数的解析式是y=

,
代入得:k=-3

,
即y=-
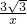
,
故答案为:y=-
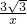
.
点评:本题考查了折叠性质,菱形性质,等边三角形的性质和判定的应用,主要考查学生的计算能力,题目比较好,有一定的难度.

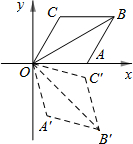
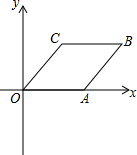 如图,菱形OABC的顶点O是坐标原点,顶点A在x轴的正半轴上,顶点B、C均在第一象限,OA=2,∠AOC=60°.点D在边AB上,将四边形OABC沿直线0D翻折,使点B和点C分别落在这个坐标平面的点B′和C′处,且∠C′DB′=60°.若某反比例函数的图象经过点B′,则这个反比例函数的解析式为________.
如图,菱形OABC的顶点O是坐标原点,顶点A在x轴的正半轴上,顶点B、C均在第一象限,OA=2,∠AOC=60°.点D在边AB上,将四边形OABC沿直线0D翻折,使点B和点C分别落在这个坐标平面的点B′和C′处,且∠C′DB′=60°.若某反比例函数的图象经过点B′,则这个反比例函数的解析式为________.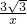
 ),设经过点B′反比例函数的解析式是y=
),设经过点B′反比例函数的解析式是y= ,代入求出即可.
,代入求出即可.
 ,OE=2+1=3,
,OE=2+1=3, ),
), ,
, ,
,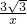 ,
,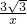 .
.

 如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置,若OB=2
如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置,若OB=2 (2013•兰州一模)如图,菱形OABC的顶点B在y轴上,顶点C的坐标为(-3,2),若反比例函数y=
(2013•兰州一模)如图,菱形OABC的顶点B在y轴上,顶点C的坐标为(-3,2),若反比例函数y= (2013•重庆)如图,菱形OABC的顶点O是坐标原点,顶点A在x轴的正半轴上,顶点B、C均在第一象限,OA=2,∠AOC=60°.点D在边AB上,将四边形OABC沿直线0D翻折,使点B和点C分别落在这个坐标平面的点B′和C′处,且∠C′DB′=60°.若某反比例函数的图象经过点B′,则这个反比例函数的解析式为
(2013•重庆)如图,菱形OABC的顶点O是坐标原点,顶点A在x轴的正半轴上,顶点B、C均在第一象限,OA=2,∠AOC=60°.点D在边AB上,将四边形OABC沿直线0D翻折,使点B和点C分别落在这个坐标平面的点B′和C′处,且∠C′DB′=60°.若某反比例函数的图象经过点B′,则这个反比例函数的解析式为 如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O逆时针旋转105°至OA′B′C′的位置.若OB=4
如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O逆时针旋转105°至OA′B′C′的位置.若OB=4