
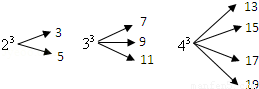
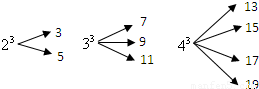
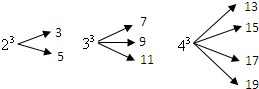 一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若63也按照此规律来进行“分裂”,则63“分裂”出的奇数中,最大的奇数是
一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若63也按照此规律来进行“分裂”,则63“分裂”出的奇数中,最大的奇数是 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
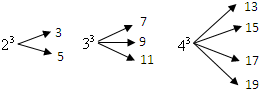 (2012•菏泽)一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若63也按照此规律来进行“分裂”,
(2012•菏泽)一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若63也按照此规律来进行“分裂”,查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•金平区模拟)一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若73也按照此规律来进行“分裂”,则73“分裂”出的奇数中,最大的奇数是
(2013•金平区模拟)一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若73也按照此规律来进行“分裂”,则73“分裂”出的奇数中,最大的奇数是查看答案和解析>>
科目:初中数学 来源: 题型:
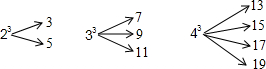
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(山东菏泽卷)数学(解析版) 题型:填空题
一个自然数的立方,可以分裂成若干个连续奇数的和.例如: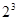 ,
,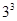 和
和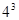 分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即
分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即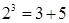 ;
;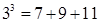 ;
;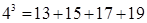 ;……;
;……;
若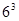 也按照此规律来进行“分裂”,则
也按照此规律来进行“分裂”,则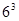 “分裂”出的奇数中,最大的奇数是 ▲ .
“分裂”出的奇数中,最大的奇数是 ▲ .
查看答案和解析>>
科目:初中数学 来源:2012-2013学年重庆市南开中学九年级(上)期初摸底数学试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com