
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+3经过点A(﹣1,0)和点B(3,0),该抛物线对称轴上的点P在x轴上方,线段PB绕着点P逆时针旋转90°至PC(点B对应点C),点C恰好落在抛物线上.
(1)求抛物线的表达式并写出抛物线的对称轴;
(2)求点P的坐标;
(3)点Q在抛物线上,联结AC,如果∠QAC=∠ABC,求点Q的坐标.
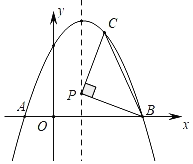
【答案】(1)y=﹣x2+2x+3,x=1;(2)(1,1);(3)(![]() ,﹣
,﹣![]() )
)
【解析】
(1)将点A、B坐标代入抛物线表达式,即可求解;
(2)证明△PMC≌△BNP(AAS),则PM=BN,MC=PN,即可求解;
(3)设MH=3x,用x表示AM、GM,利用AG=AM+GM=![]() ,求出x的值;在△AOH中,OH=
,求出x的值;在△AOH中,OH=![]() ,求得点H的坐标,即可求解.
,求得点H的坐标,即可求解.
(1)将点A、B坐标代入抛物线表达式得:![]() ,解得:
,解得:![]() ,
,
故抛物线的表达式为:y=﹣x2+2x+3①;
函数的对称轴为:x=1;
(2)设点C(m,n),则n=﹣m2+2m+3,点P(1,s),
如图1,设抛物线对称轴交x轴于点N,过点C作CM⊥PN交抛物线对称轴于点M,
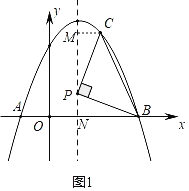
∵∠PBN+∠BPN=90°,∠BPN+∠MPC=90°,
∴∠MPC=∠PBN,
∵∠PMC=∠BNP=90°,PB=PC,
∴△PMC≌△BNP(AAS),
∴PM=BN,MC=PN,
∴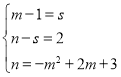 ,解得:
,解得: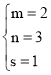 ,
,
故点C(2,3),点P(1,1);
故点P的坐标为(1,1);
(3)设直线AC交y轴于点G,直线AQ交y轴于点H,
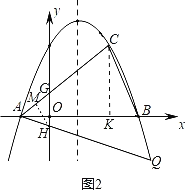
由(2)知,点C(2,3),而点A(﹣1,0),
过点C作CK⊥x轴于点K,则CK=AK=3,
故直线AC的倾斜角为45°,故∠AGO=∠GAO=45°,
∴tan∠ABC=![]() =3
=3
∵∠QAC=∠ABC,
∴tan∠QAC=3;
在△AGH中,过点H作HM⊥AG于点M,设MH=3x,
∵∠AGO=45°,则GO=AO=1,
∴MG=MH=3x,
∵tan∠QAC=3,则AM=x,
AG=AM+GM=x+3x=![]() =
=![]() ,
,
解得:x=![]() ,
,
在△AHM中,AH=![]() =
=![]() x=
x=![]() ,
,
在△AOH中,OH=![]() =
=![]() ,故点H(0,﹣
,故点H(0,﹣![]() ),
),
由点A、H的坐标得,直线AH的表达式为:y=﹣![]() x﹣
x﹣![]() ②,
②,
联立①②并解得:x=﹣1(舍去)或![]() ,
,
故点Q的坐标为:(![]() ,﹣
,﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,某二次函数的图象是一条顶点为P(4.-4)的抛物线,它经过原点和点A,它的对称轴交线段
OA于点M.点N在对移轴上,且点M、N关于点P对称,连接AN,ON
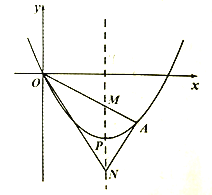
(1)求此二次函数的解析式:
(2)若点A的坐标是(6,-3).,请直接写出MN的长
(3)若点A在抛物线的对称轴右侧运动时,则∠ANM与∠ONM有什么数量关系?并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】书法是我国的文化瑰宝,研习书法能培养高雅的品格.某校为加强书法教学,了解学生现有的书写能力,随机抽取了部分学生进行测试,测试结果分为优秀、良好、及格、不及格四个等级,分别用A,B,C,D表示,并将测试结果绘制成如图两幅不完整的统计图.
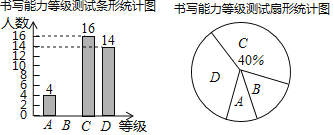
请根据统计图中的信息解答以下问题:
(1)本次抽取的学生人数是 ,扇形统计图中A所对应扇形圆心角的度数是 .
(2)把条形统计图补充完整.
(3)若该学校共有2800人,等级达到优秀的人数大约有多少?
(4)A等级的4名学生中有3名女生1名男生,现在需要从这4人中随机抽取2人参加电视台举办的“中学生书法比赛”,请用列表或画树状图的方法,求被抽取的2人恰好是1名男生1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
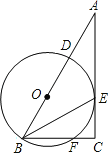
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
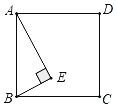
【题目】如图,在正方形ABCD中,AB=10,点E在正方形内部,且AE⊥BE,cot∠BAE=2,如果以E为圆心,r为半径的⊙E与以CD为直径的圆相交,那么r的取值范围为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
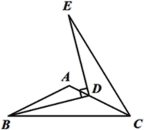
【题目】如图,在△ABC中,AB=AC=10,BC=![]() ,D为边AC上一动点(C点除外),把线段BD绕着点D沿着顺时针的方向旋转90°至DE,连接CE,则△CDE面积的最大值为______.
,D为边AC上一动点(C点除外),把线段BD绕着点D沿着顺时针的方向旋转90°至DE,连接CE,则△CDE面积的最大值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
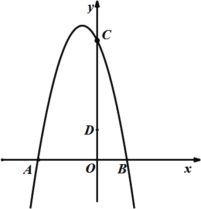
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点A、B,与
轴交于点A、B,与![]() 轴交于点C,点B的坐标为
轴交于点C,点B的坐标为![]() ,点
,点![]() 在
在![]() 轴上,连接AD.
轴上,连接AD.
(1)![]() = ;
= ;
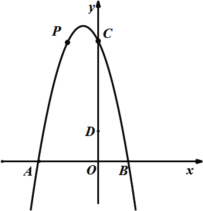
(2)若点![]() 是抛物线在第二象限上的点,过点
是抛物线在第二象限上的点,过点![]() 作PF⊥x轴,垂足为
作PF⊥x轴,垂足为![]() ,
,![]() 与
与![]() 交于点E.是否存在这样的点P,使得PE=7EF?若存在,求出点
交于点E.是否存在这样的点P,使得PE=7EF?若存在,求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)若点![]() 在抛物线上,且点
在抛物线上,且点![]() 的横坐标大于-4,过点
的横坐标大于-4,过点![]() 作
作![]() ,垂足为H,直线
,垂足为H,直线![]() 与
与![]() 轴交于点K,且
轴交于点K,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
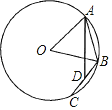
【题目】如图,已知⊙O的半径为6,点A、B在⊙O上,∠AOB=60°,动点C在⊙O上(与A、B两点不重合),连接BC,点D是BC中点,连接AD,则线段AD的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com