
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |

(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8)
【答案】(1)甲测试成绩的众数和中位数都是7分;(2)选乙运动员更合适.
【解析】试题分析:试题分析:(1)观察表格可知甲运动员测试成绩的众数和中位数都是7;
(2)易知![]() =7(分),
=7(分),![]() =7(分),
=7(分),![]() =6.3(分),结合题中所给的方差即可进行判断.
=6.3(分),结合题中所给的方差即可进行判断.
试题解析:(1)甲运动员测试成绩中7出现最多,故甲的众数为7;
甲成绩重新排列为:5、6、7、7、7、7、7、8、8、8,
∴甲的中位数为![]() =7,
=7,
∴甲测试成绩的众数和中位数都是7分;
(2)![]() =
=![]() ×(7+6+8+7+7+5+8+7+8+7)=7,
×(7+6+8+7+7+5+8+7+8+7)=7,
![]() =
=![]() ×(6+6+7+7+7+7+7+7+8+8)=7,
×(6+6+7+7+7+7+7+7+8+8)=7,
![]() =
=![]() ×(5×2+6×4+7×3+8×1)=6.3,
×(5×2+6×4+7×3+8×1)=6.3,
∵![]() =
= ![]() ,S甲2>S乙2,
,S甲2>S乙2,
∴选乙运动员更合适.


科目:初中数学 来源: 题型:
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD
BD
其中正确结论的为______(请将所有正确的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年2月初,合肥市教育考试院召开新闻发布会,公布了合肥市市区参加2016年中考的学生约为27600人,与去年相比增加300多人,用科学记数法表示“27600”正确的( )
A.2.76×103
B.2.76×104
C.2.76×105
D.0.276×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一段圆柱体的树干的示意图,已知树干的半径r=10cm,AD=45cm. (π值取3)
(1)若螳螂在点A处,蝉在点C处,图1中画出了螳螂捕蝉的两条路线,即A→D→C和A→C,图2是该圆柱体的侧面展开图,判断哪条路的距离较短,并说明理由;
(2)若螳螂在点A处,蝉在点D处,螳螂想要捕到这只蝉,但又怕蝉发现,于是螳螂绕到
后方去捕捉它,如图3所示,求螳螂爬行的最短距离;(提示: ![]() =75)
=75)
(3)图4是该圆柱体的侧面展开图,蝉N在半径为10cm的⊙O的圆上运动,⊙O与BC相切,点O到CD的距离为20cm,螳螂M在线段AD运动上,连接MN,MN即为螳螂捕蝉时螳螂爬行的距离,若要使MN与⊙O总是相切,求MN的长度范围.

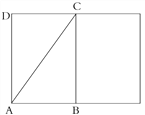


图1 图2 图3 图4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某城市规定用水收费标准如下:每户每月用水不超过6m3,水费按1.6元/m3收费;每户每月用水超过6m3时,超过的部分按4元/m3收费.设每户每月用水量为x(m3),应缴水费为y元.
(1)写出每月用水不超过6m3和超过6m3时,y与x之间的函数关系式.
(2)已知某户5月份的用水量为8m3,求该用户5月份的水费.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com