解:(1)由题意可知,m(m+1)=(m+3)(m-1),解得m=3,
∴A(3,4),B(6,2),
∴k=4×3=12;
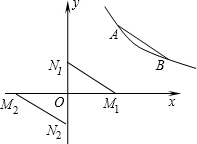
(2)存在两种情况,如图:
①当M点在x轴的正半轴上,N点在y轴的正半轴上时,设M
1点坐标为(x
1,0),
N
1点坐标为(0,y
1),
∵四边形AN
1M
1B为平行四边形,
∴线段N
1M
1可看作由线段AB向左平移3个单位,再向下平移2个单位得到的,
(也可看作向下平移2个单位,再向左平移3个单位得到的)
由(1)知A点坐标为(3,4),B点坐标为(6,2),
∴N
1点坐标为(0,4-2),即N
1(0,2),
M
1点坐标为(6-3,0),即M
1(3,0),
设直线M
1N
1的函数表达式为y=k
1x+2,
把x=3,y=0代入,解得
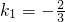
,
∴直线M
1N
1的函数表达式为
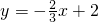
;
②当M点在x轴的负半轴上,N点在y轴的负半轴上时,
设M
2点坐标为(x
2,0),N
2点坐标为(0,y
2),
∵AB∥N
1M
1,AB∥M
2N
2,AB=N
1M
1,AB=M
2N
2,
∴N
1M
1∥M
2N
2,N
1M
1=M
2N
2,
∴四边形N
1M
2N
2M
1为平行四边形,
∴点M
1、M
2与线段N
1、N
2关于原点O成中心对称,
∴M
2点坐标为(-3,0),N
2点坐标为(0,-2),
设直线M
2N
2的函数表达式为y=k
2x-2,
把x=-3,y=0代入,解得

,
∴直线M
2N
2的函数表达式为

.
所以,直线MN的函数表达式为
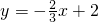
或

.
分析:(1)求m、k两个未知字母,把A、B两点代入反比例函数即可;
(2)按图中所给情况,M、N有可能都在坐标轴的正半轴,也有可能在坐标轴的负半轴,平移应找到对应点,看是如何平移得到.求出直线MN的函数表达式,需求出A,B两点的坐标.
点评:过某个点,这个点的坐标应适合这个函数解析式.平行四边形从动态来看也可以是由一条线段平移得到的.

 如图,点A(m,m+1),B(m+3,m-1)都在反比例函数
如图,点A(m,m+1),B(m+3,m-1)都在反比例函数 的图象上.
的图象上. 解:(1)由题意可知,m(m+1)=(m+3)(m-1),解得m=3,
解:(1)由题意可知,m(m+1)=(m+3)(m-1),解得m=3,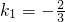 ,
,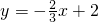 ;
; ,
, .
.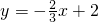 或
或 .
.

 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°. 如图,点A的坐标为(2
如图,点A的坐标为(2