
为了顾及鱼塘中的鱼数,养鱼者首先从鱼塘中打捞



 ,你认为这种估计方法有道理吗?为什么?
,你认为这种估计方法有道理吗?为什么?
科目:初中数学 来源:内蒙古巴彦淖尔市杭锦全旗2018届九年级中考数学一模试卷 题型:解答题
阅读
(1)阅读理【解析】

如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是________;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源:2018年秋北师大版七年级数学上册 第二章 有理数及其运算 达标测试卷 题型:解答题
如图,数轴上的点A,B,C分别表示数-3,-1,2.
(1)A,B两点间的距离AB=________,A,C两点间的距离AC=________.
(2)若点E表示的数为x,则AE的长等于多少?
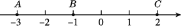
查看答案和解析>>
科目:初中数学 来源:2018年秋北师大版七年级数学上册 第二章 有理数及其运算 达标测试卷 题型:单选题
学校、文具店、书店依次坐落在一条南北走向的大街上,学校在文具店的南边20 m处,书店在文具店的北边100 m处,张明同学从文具店出发,向北走了50 m,接着又向北走了-70 m,此时张明的位置在( )
A. 文具店 B. 学校 C. 书店 D. 以上都不对
查看答案和解析>>
科目:初中数学 来源:苏科版九年级数学下册_第八章_统计和概率的简单应用_单元检测试卷 题型:解答题
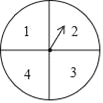
由于只有1张市运动会开幕式的门票,小王和小张都想去,两人商量采取转转盘(如图,转盘盘面被分为面积相等,且标有数字1,2,3,4的4个扇形区域)的游戏方式决定谁胜谁去观看.规则如下:两人各转动转盘一次,当转盘停止转动时,如两次指针对应盘面数字都是奇数,则小王胜;如两次指针对应盘面数字都是偶数,则小张胜;如两次指针对应盘面数字是一奇一偶,则视为平局.若为平局,继续上述游戏,直至分出胜负.
若小王和小张按上述规则各转动转盘一次,则
(1)小王转动转盘,当转盘停止转动时,对应盘面数字为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树状图的方法说明理由.
查看答案和解析>>
科目:初中数学 来源:苏科版九年级数学下册_第八章_统计和概率的简单应用_单元检测试卷 题型:填空题
有一箱规格相同的红、黄两种颜色的小塑料球共1000个.为了估计这两种颜色的球各有多少个,小明将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后.发现摸到红球的频率约为0.6,据此可以估计红球的个数约为________.
查看答案和解析>>
科目:初中数学 来源:苏科版九年级数学下册_第八章_统计和概率的简单应用_单元检测试卷 题型:单选题
在一个不透明的布袋中装有红色、白色玻璃球共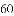
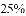
A. 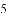
查看答案和解析>>
科目:初中数学 来源:山东省2018-2019学年度第一学期北师大版七年级数学上册第一章丰富的图形世界第一周周周清测试卷 题型:填空题
如图,这个图形从正面看是________,从左面看是________,从上面看是________.

查看答案和解析>>
科目:初中数学 来源:江苏省宜兴市周铁学区2018-2019学年八年级上学期期中考试数学试卷 题型:解答题
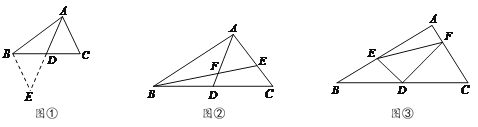
(问题情境)
课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=10,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB,依据是( ).
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
(初步运用)
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=4,EC=3,求线段BF的长.
(灵活运用)
如图③,在△ABC中,∠A=90°,D为BC中点, DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com