怎样的整数a、b满足不等式a2+3b2+6<2ab-8b?
【答案】
分析:先把不等式a
2+3b
2+6<2ab-8b变形得到(a-b)
2+2(b+2)
2<2,因为a,b都为整数,所以只有(a-b)
2=0,2(b+2)
2=0或(a-b)
2=1,2(b+2)
2=0两种情况,从而可求解.
解答:证明:∵a
2+3b
2+6<2ab-8b
∴a
2-2ab+b
2+2b
2+8b+6<0
(a-b)
2+2(b+2)
2<2(3分)
∵a,b均为整数,
∴只有(a-b)
2=0,2(b+2)
2=0或(a-b)
2=1,2(b+2)
2=0两种情况.(2分)
(1)当(a-b)
2=0,2(b+2)
2=0时,
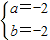
(2分)
(2)当(a-b)
2=1,2(b+2)
2=0时,
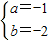
,
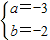
(2分)
综上,当
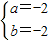
,
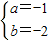
,
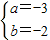
时,原不等式成立.(1分)
点评:本题考查整数问题的综合运用,关键是把不等式进行变形后,根据变形后得特点和a,b都是整数可求得解.

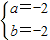 (2分)
(2分)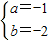 ,
,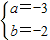 (2分)
(2分)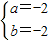 ,
,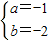 ,
,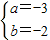 时,原不等式成立.(1分)
时,原不等式成立.(1分)
