
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB:OE=3:2.其中正确结论的个数是 ( )

A.1 B.2 C.3 D.4
【答案】C.
【解析】
试题解析:连接BD,

∵四边形ABCD是矩形,
∴AC=BD,AC、BD互相平分,
∵O为AC中点,
∴BD也过O点,
∴OB=OC,
∵∠COB=60°,OB=OC,
∴△OBC是等边三角形,
∴OB=BC=OC,∠OBC=60°,
在△OBF与△CBF中
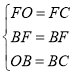
∴△OBF≌△CBF(SSS),
∴△OBF与△CBF关于直线BF对称,
∴FB⊥OC,OM=CM;
∴①正确,
∵∠OBC=60°,
∴∠ABO=30°,
∵△OBF≌△CBF,
∴∠OBM=∠CBM=30°,
∴∠ABO=∠OBF,
∵AB∥CD,
∴∠OCF=∠OAE,
∵OA=OC,
易证△AOE≌△COF,
∴OE=OF,
∴OB⊥EF,
∴四边形EBFD是菱形,
∴③正确,
∵△EOB≌△FOB≌△FCB,
∴△EOB≌△CMB错误.
∴②错误,
∵∠OMB=∠BOF=90°,∠OBF=30°,
∴MB=![]() ,OF=
,OF=![]() ,
,
∵OE=OF,
∴MB:OE=3:2,
∴④正确;
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径r=25,四边形ABCD内接圆⊙O,AC⊥BD于点H,P为CA延长线上的一点,且∠PDA=∠ABD
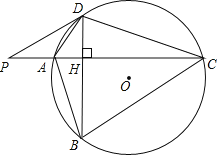
(1) 试判断PD与⊙O的位置关系,并说明理由
(2) 若tan∠ADB=![]() ,PA=
,PA=![]() AH,求BD的长
AH,求BD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
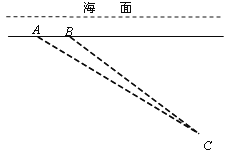
【题目】如图,一艘潜艇在海面下500米深处的A点,测得正前方俯角为31.0°方向上的海底有黑匣子发出的信号,潜艇在同一深度保持直线航行500米,在B点处测得海底黑匣子位于正前方俯角为36.9°的方向上,求海底黑匣子C所在点距离海面的深度.(精确到1米)(参考数据:sin36.9° ≈ 0.60,cos36.9° ≈ 0.80,tan36.9° ≈0.75,sin31.0°≈ 0.51,cos31.0°≈0.87 ,tan31.0°≈ 0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于条形统计图、折线统计图和扇形统计图这三种常见的统计图,下列说法正确的是( )
A. 条形统计图能清楚地反映事物的变化情况
B. 折线统计图能清楚地表示出每个项目的具体数目
C. 扇形统计图能清楚地表示出各部分在总体中所占的百分比
D. 三种统计图不可互相转换
查看答案和解析>>
科目:初中数学 来源: 题型:
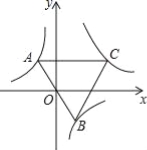
【题目】如图,已知点A是双曲线y=-![]() 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第一象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第一象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=![]() (k>0)上运动,则k的值是 .
(k>0)上运动,则k的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若△ABC∽△A′B′C′,相似比为1∶3,则△ABC与△A′B′C′的面积的比为( )
A. 1∶3 B. 3∶1 C. 4∶1 D. 1∶9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com