(1)①证明:在Rt△ABC中,
∵∠B=30°,AB=10,
∴∠CAB=60°,AC=

AB=5,
∵点F是AB的中点,
∴AF=

AB=5,
∴AC=AF,
∵△ADE是等边三角形,
∴AD=AE,∠EAD=60°,
∵∠CAB=∠EAD,即∠CAD+∠DAB=∠FAE+∠DAB,
∴∠CAD=∠FAE,
在△AEF和△ADC中,

,
∴△AEF≌△ADC(SAS);
②∵△AEF≌△ADC,
∴∠AEF=∠C=90°,EF=CD=x,
又∵点F是AB的中点,
∴AE=BE=y,
在Rt△AEF中,勾股定理可得:y
2=25+x
2,
∴函数的解析式是y=
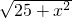
,定义域是0<x≤5

;
(2)①当点在线段CB上时,
由∠DAB=15°,可得∠CAD=45°,△ADC是等腰直角三角形,
∴AD
2=50,
△ADE的面积为
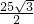
;
②当点在线段CB的延长线上时,
由∠DAB=15°,可得∠ADB=15°,BD=BA=10,
∴在Rt△ACD中,勾股定理可得AD2=200+100

,
△ADE的面积为50

+75,
综上所述,△ADE的面积为
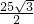
或50

+75.
分析:(1)①在直角三角形ABC中,由30度所对的直角边等于斜边的一半求出AC的长,再由F为AB中点,得到AC=AF=5,确定出三角形ADE为等边三角形,利用等式的性质得到一对角相等,砸由AD=AE,利用SAS即可得证;
②由全等三角形对应角相等得到∠AEF为直角,EF=CD=x,在三角形AEF中,利用勾股定理即可列出y关于x的函数解析式及定义域;
(2)分两种情况考虑:①当点在线段CB上时;②当点在线段CB的延长线上时,分别求出三角形ADE面积即可.
点评:此题考查了勾股定理,全等三角形的判定与性质,以及等边三角形的性质,熟练掌握勾股定理是解本题的关键.

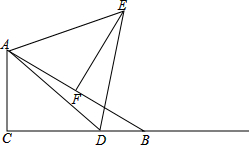 在Rt△ABC中,∠C=90°,∠B=30°,AB=10,点D是射线CB上的一个动点,△ADE是等边三角形,点F是AB的中点,联结EF.
在Rt△ABC中,∠C=90°,∠B=30°,AB=10,点D是射线CB上的一个动点,△ADE是等边三角形,点F是AB的中点,联结EF. AB=5,
AB=5, AB=5,
AB=5, ,
,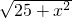 ,定义域是0<x≤5
,定义域是0<x≤5 ;
;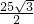 ;
; ,
, +75,
+75,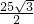 或50
或50 +75.
+75.

 阅读快车系列答案
阅读快车系列答案