
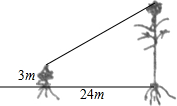
 有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m远的一棵大树上,大树高14m,且巢离树顶部1m,当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5m/s,那它至少需要多少时间才能赶回巢中?(画出符合题意的几何图形,并求解)
有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m远的一棵大树上,大树高14m,且巢离树顶部1m,当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5m/s,那它至少需要多少时间才能赶回巢中?(画出符合题意的几何图形,并求解) 科目:初中数学 来源: 题型:选择题
 如图,△ABC中,边BC=12,高AD=6.矩形MNPQ的边在BC上,顶点P在AB上,顶点N在AC上,若S矩形MNPQ=y,PN=x,则y与x的关系式为( )
如图,△ABC中,边BC=12,高AD=6.矩形MNPQ的边在BC上,顶点P在AB上,顶点N在AC上,若S矩形MNPQ=y,PN=x,则y与x的关系式为( )| A. | y=6-$\frac{1}{2}$x(0<x<12) | B. | y=-$\frac{1}{2}$x2+6x(0<x<12) | ||
| C. | y=2x2-12x(0<x<12) | D. | y=$\frac{1}{2}$x2+6x(0<x<12) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-(y+z)2 | B. | (x-y)2-z2 | C. | -(x-y)2+z2 | D. | x2-(y-z)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上.已知正方形A1B1C1D1的边长为1,∠C1B1O=30°,B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是( )
在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上.已知正方形A1B1C1D1的边长为1,∠C1B1O=30°,B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是( )| A. | ${(\frac{1}{2})}^{2015}$ | B. | ${(\frac{1}{2})}^{2016}$ | C. | ${(\frac{\sqrt{3}}{3})}^{2015}$ | D. | ${(\frac{\sqrt{3}}{3})}^{2016}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE与BF相交于O;下列结论:
如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE与BF相交于O;下列结论:| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
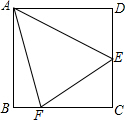 如图,在边长为$6\sqrt{2}$的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )
如图,在边长为$6\sqrt{2}$的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )| A. | $2\sqrt{2}$ | B. | 3 | C. | $3\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com