
 ,∠A=45°,以AB所在直线为x轴,A为坐标原点建立直角坐标系,将?ABCD绕A点按逆时针方向旋转90°得到?OEFG(图1)
,∠A=45°,以AB所在直线为x轴,A为坐标原点建立直角坐标系,将?ABCD绕A点按逆时针方向旋转90°得到?OEFG(图1)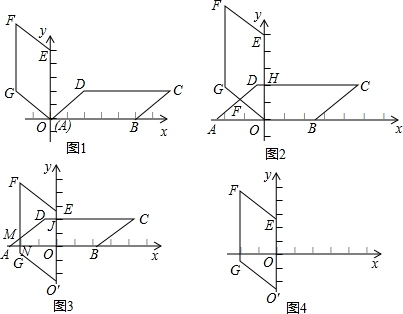
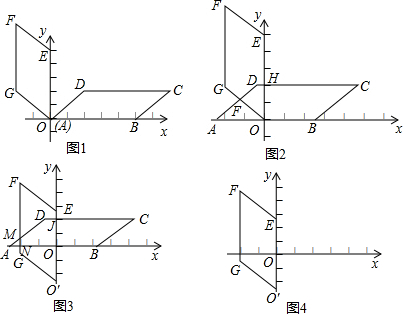
 OA=
OA= x,OH=2,DH=x-2
x,OH=2,DH=x-2 AF•
AF• y=
y=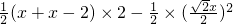 =-
=-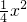 +2x-2(2<x<4)
+2x-2(2<x<4)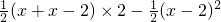
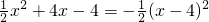 +4
+4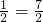

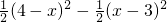 y=-x2+7x-
y=-x2+7x-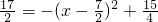
 时,
时,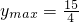
 秒时,重叠部分面积的最大值是
秒时,重叠部分面积的最大值是
 秒时,重叠部分面积的最大值是
秒时,重叠部分面积的最大值是


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com