
如图,△ABC中,∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM⊥AC于点M,BM交CD于点E,且点E为CD的中点,连接MD,过点D作ND⊥MD于点D,DN交BM于点N.
(1)若BC=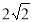 ,求△BDE的周长;
,求△BDE的周长;
(2)求证:NE-ME=CM.

(1)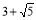 ;(2)完成证明见解析
;(2)完成证明见解析
【解析】
试题分析:(1)充分利用直角三角形的性质和勾股定理即可得解,在Rt△BDE中,要求周长,求出是BD长是关键,而BD长放在Rt△BCD中即可得解.
(2)想证明NE-ME=CM这样的关系,关键将其放入全等三角形中,用等量代换的关系即可得证,充分利用点E为CD的中点的条件作出辅助线,过D作D作DF⊥BM于点F,或过点D作DF∥CM交BM于点F,或在MB上截取EF,使EF=EM(如第24题解答图1),另外也可过点C作CP∥DN交BM延长线于点P,或过点C作CP∥DN交BM延长线于点P,或延长EM至点P,使EP=EN(如第24题解答图2),利用两次全等三角形,即可得证。
试题解析:
(1)∵∠ABC=45°,CD⊥AB
∴在Rt△BCD中,∠DBC=∠DCB=45°
∵BC=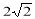 ∴BD=CD=2
∴BD=CD=2
∵点E为CD中点
∴DE=CE=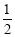 CD=1
CD=1
∴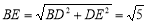
∴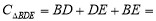
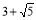
∴△BDE的周长为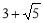

(2)(方法一)过点D作DF⊥BM于点F
∵BM⊥AC
∴∠DFE=∠CME=90°
在△DEF和△CEM中

∴△DEF≌△CEM(AAS)
∴DF=CM FE=ME
∵ND⊥MD,CD⊥AB
∴∠BDN+∠NDE=∠CDM+∠NDE=90°
∴∠BDN=∠CDM
∵CD⊥AB,BM⊥AC
∴∠BDE=∠CDA=90°
∠DBE+∠DEB=∠ACD+∠CEM=90°
∵∠DEB=∠CEM ∴∠DBE=∠ACD
在△BDN和△CDM中

∴△BDN≌△CDM(ASA)
∴DN=DM
∴在Rt△DMN中,∠DNM=∠DMN=45°
∴在Rt△DMN中,∠DNM=∠NDF=45°
∴DF=NF
又∵DF=CM,FE=ME
∴NE=NF+FE=CM+ME
∴NE-ME=CM.
(2)问其他方法:(解法略)
方法二:过点D作DF∥CM交BM于点F
方法三:在MB上截取EF,使EF=EM
方法四:过点C作CP∥DN交BM延长线于点P
方法五:延长EM至点P,使EP=EN
考点:1.直角三角形判定及性质定理;2 .全等三角形判定及性质定理.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014中考名师推荐数学三角形(一)(解析版) 题型:选择题
如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有( )
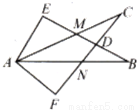
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学一元一次不等式组(解析版) 题型:选择题
若关于x的不等式组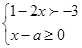 的整数解共有5个,则a的取值范围是( )
的整数解共有5个,则a的取值范围是( )
A.﹣4<a≤﹣3
B.﹣4≤a<﹣3
C.﹣4≤a≤﹣3
D.﹣4<a<﹣3
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省大庆市九年级下学期期末数学试卷(解析版) 题型:选择题
在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在15%和45%,则口袋中白色球的个数可能是( )
A.24 B.18 C.16 D.6
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省大庆市九年级下学期期末数学试卷(解析版) 题型:选择题
如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG= ,则△CEF的面积是( )
,则△CEF的面积是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题(一)数学试卷(解析版) 题型:选择题
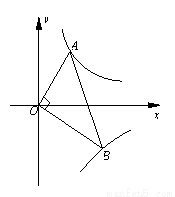
已知点A、B分别在反比例函数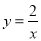 (x>0),
(x>0),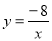 (x>0)的图象上,且OA⊥OB,则
(x>0)的图象上,且OA⊥OB,则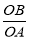 的值为( )
的值为( )
A.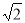 B.2 C.
B.2 C.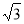 D.3
D.3
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题二数学试卷(解析版) 题型:选择题
下列说法不正确的是( ).
A.选举中,人们通常最关心的数据是众数
B.要了解一批烟花的燃放时间,应采用抽样调查的方法
C.若甲组数据的方差 ,乙组数据的方差
,乙组数据的方差 ,则甲组数据比乙组数据稳定
,则甲组数据比乙组数据稳定
D.某抽奖活动的中奖率是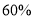 ,说明参加该活动10次就有6次会中奖
,说明参加该活动10次就有6次会中奖
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com