
 如图,∠AOB=30°,点P是∠AOB内一点,PO=8,在∠AOB的两边上分别有点R、Q均不同于O).
如图,∠AOB=30°,点P是∠AOB内一点,PO=8,在∠AOB的两边上分别有点R、Q均不同于O).分析 (1)根据轴对称图形的性质,作出P关于OA、OB的对称点M、N,连接MN,根据两点之间线段最短得到最小值线段,根据等边三角形的性质解答即可;
(2)根据对称的性质求得∠OMN+∠ONM=∠OPQ+∠OPR,即可求得∠QPR的度数.
解答 解:(1)分别作P关于OA、OB的对称点M、N.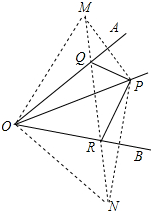
连接MN交OA、OB交于Q、R,则△PQR符合条件.
连接OM、ON,
由轴对称的性质可知,OM=ON=OP=8,
∠MON=∠MOP+∠NOP=2∠AOB=2×30°=60°,
则△MON为等边三角形,
∴MN=8,
∵QP=QM,RN=RP,
∴△PQR周长=MN=8,
(2)根据对称的性质得到∠OMN=∠OPQ,∠ONM=∠OPR,
∴∠OMN+∠ONM=∠OPQ+∠OPR,
∵△MON为等腰直角三角形,
∴∠OMN+∠ONM=120°,
∴∠OPQ+∠OPR=120°,
即∠QPR=120°
点评 本题考查了轴对称-最短路径问题,根据轴对称的性质作出对称点是解题的关键,掌握线段垂直平分线的性质和等边三角形的性质的灵活运用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com