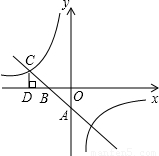
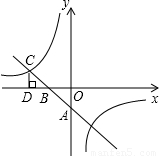
(2005•南充)如图,已知抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,与y轴交于点M,与x轴交于点A和B.
(1)y=mx2+nx+p的解析式为______,试猜想出与一般形式抛物线y=ax2+bx+c关于y轴对称的二次函数解析式为______.
(2)A,B的中点是点C,则sin∠CMB=______
【答案】
分析:(1)抛物线y=mx
2+nx+p与y=x
2+6x+5关于y轴对称,即y=x
2+6x+5上的点关于y轴的对称点在函数y=mx
2+nx+p上,可以在y=x
2+6x+5上取几点,求出它们关于y轴的对称点,利用待定系数就可以求出函数的解析式.
(2)根据抛物线的解析式,可以求出A,B点的坐标,则C的坐标也可以求出.过点C作CD⊥BM,易证,△BCD是等腰直角三角形,在直角△BCD中根据三角函数可以求出CD,在直角△NOC中,根据勾股定理就可以求出MC的长,则sin∠CMB就可以求出.
(3)设过点M(0,5)的直线为y=kx+b,则b=5.则直线的解析式是y=kx+5,与抛物线的解析式组成方程组,解方程组就可以得到N,M两点的坐标,可以得到a,b的关系,从而求出值.
解答:解:(1)y=x
2+6x+5的顶点为(-3,-4),
即y=mx
2+nx+p的顶点的为(3,-4),
设y=mx
2+nx+p=a(x-3)
2-4,
y=x
2+6x+5与y轴的交点M(0,5),
即y=mx
2+nx+p与y轴的交点M(0,5).
即a=1,
所求二次函数为y=x
2-6x+5.
猜想:
与一般形式抛物线y=ax
2+bx+c关于y轴对称的二次函数解析式是y=ax
2-bx+c.
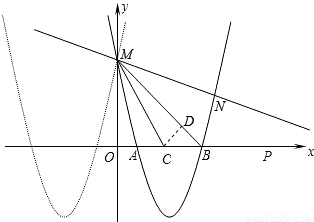
(2)过点C作CD⊥BM.
抛物线y=x
2-6x+5与x轴的交点A(1,0),B(5,0),与y轴交点M(0,5),AB中点C(3,0).
故△MOB,△BCD是等腰直角三角形,CD=
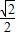
BC=
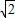
.
在Rt△MOC中,MC=
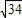
.
则sin∠CMB=
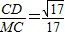
.
(3)设过点M(0,5)的直线为y=kx+b,则b=5.
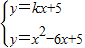
,
解得
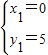
,
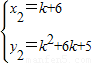
,
则a=k+6,b=k
2+6k+5,
由已知a,b是方程x
2-x+m=0的解,故a+b=1.
即(k+6)+(k
2+6k+5)=1,
化简k
2+7k+10=0,则k
1=-2,k
2=-5.
点N的坐标是(4,-3)或(1,0).
点评:本题主要考查了关于y轴对称的函数解析式的关系,已知一个函数的解析式,利用-x代替式子中的x,就可以得到函数关于y轴
对称的函数的解析式.


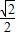 BC=
BC=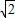 .
.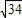 .
.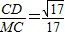 .
.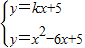 ,
,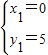 ,
,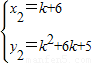 ,
,

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案